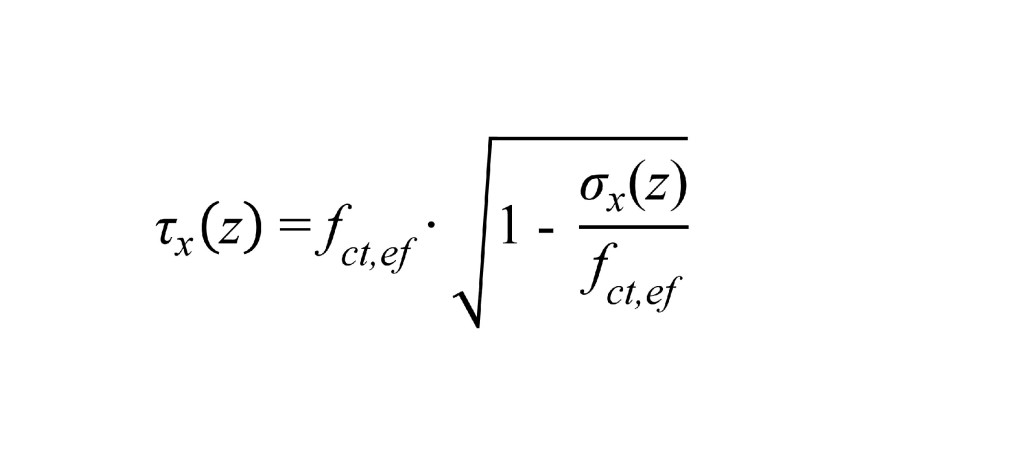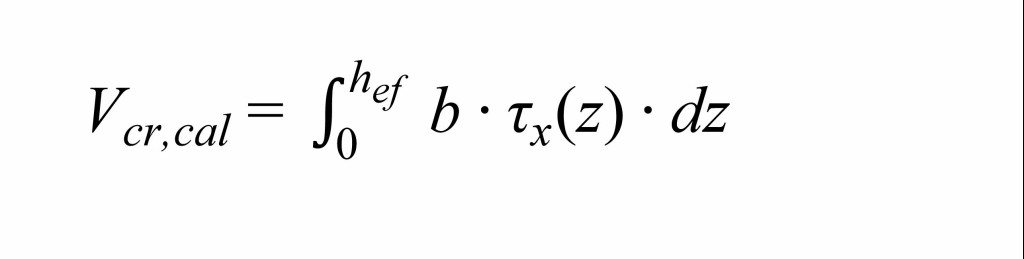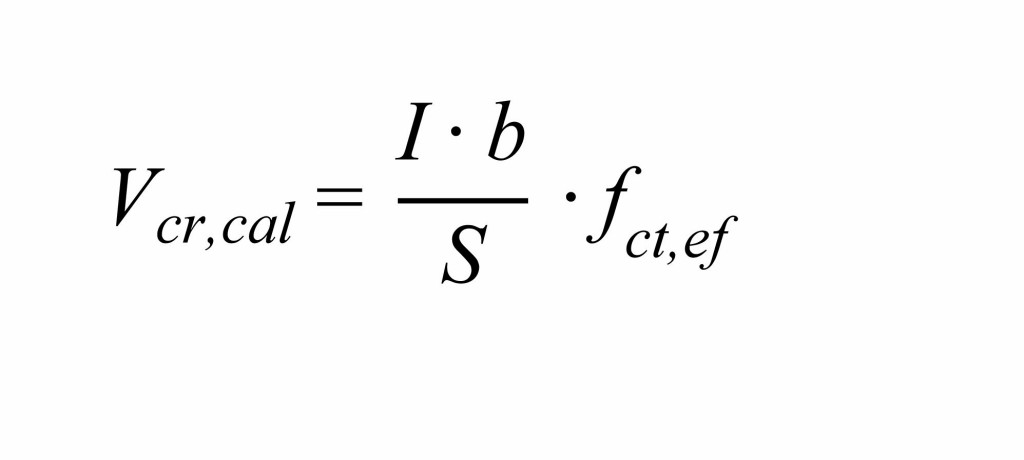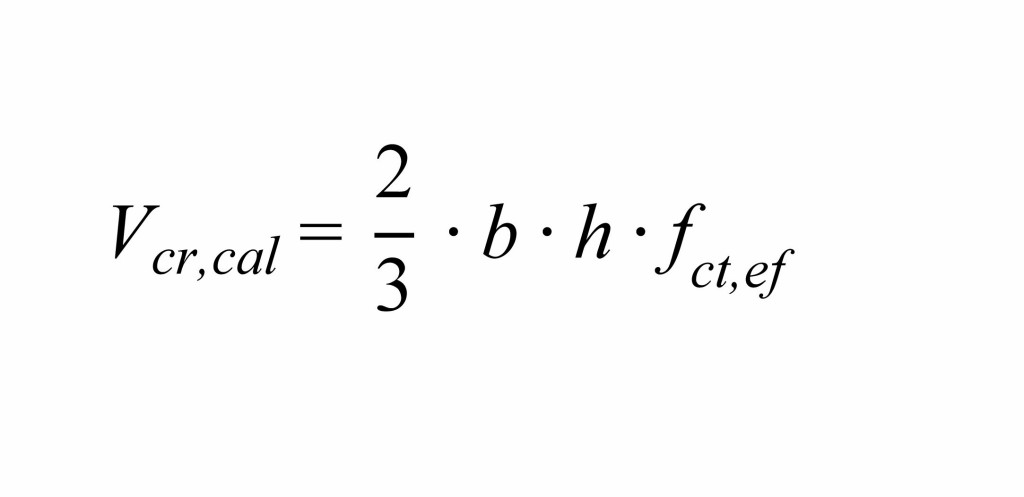Schrägrissbildung von Stahlbetonbalken unter Querkraftbeanspruchung

 

Foto: PantherMedia / Fahroni

Im Rahmen des DFG geförderten Graduiertenkollegs 2075 wurde deshalb am iBMB, Fachgebiet Massivbau der TU Braunschweig die Querkraftdatenbank nach DAfStb-Heft 597 um die experimentellen Schrägrisslasten erweitert und hinsichtlich verschiedener Einflussparameter wie Schubschlankheit, Längsbewehrungsgrad und Betonfestigkeit auf den Betonzugtraganteil unter Querkraftbeanspruchung untersucht. Die Anwendbarkeit der in der Fachliteratur vorhandenen mechanisch begründeten Modelle wurde anhand der erweiterten Datenbank untersucht. Auf Basis der Untersuchungen konnte ein geeignetes Modell zur Ermittlung der Schrägrisslast von Stahlbetonbauteilen verifiziert und im Anschluss ein vereinfachtes ingenieurmäßiges Modell vorgeschlagen werden.

1 Einleitung

Für die Zustandsbewertung vieler älterer Stahlbeton- und Spannbetonbrücken in Deutschland spielt die Querkrafttragfähigkeit eine wichtige Rolle. Die bisher durchgeführten Nachrechnungen nach der Nachrechnungsrichtlinie [1] zeigen oft rechnerische Querkraftdefizite. Aus einem im Auftrag der Bundesanstalt für Straßenwesen initiierten Forschungsvorhaben [2] wurden erweiterte Verfahren zum Nachweis der Querkraft- und Torsionstragfähigkeit untersucht und nachfolgend in die 1. Ergänzung der Nachrechnungsrichtlinie [3] aufgenommen, darunter auch das sogenannte Hauptzugspannungskriterium. Dieses sieht für ungerissene Querschnitte eine Ermittlung der Spannungsverteilung im Betonquerschnitt auf Grundlage der technischen Biegetheorie vor. Hierzu müssen zum einen nicht durch konzentrierte Lasten gestörte Spannungsbereiche und zum anderen linearelastisches Materialverhalten vorliegen. Aus Letzterem folgt, dass die Hauptzugspannungsformel nur in Bereichen angewendet werden darf, in denen im Grenzzustand der Tragfähigkeit keine Risse auftreten [4], [5], [6], [7]. Unter dieser Voraussetzung ist es wichtig, die Rissbildung in den relevanten Nachweisbereichen abschätzen zu können.

Bestehende Bauwerke liefern in diesem Zusammenhang im Allgemeinen keinen Beitrag, da nach [5] hier oft keine Schrägrisse erkennbar sind. In [7] wird zudem berichtet, dass der rechnerisch ermittelte schrägrissgefährdete Bereich oft nicht mit den während einer Bauwerksprüfung visuell aufgenommenen Rissen übereinstimmt. Im Umkehrschluss lässt sich daraus schließen, dass unter anderem die tatsächliche Schrägrisslast sowie der Betonzugtraganteil durch die vorhandenen Berechnungsansätze unterschätzt wird.

Innerhalb des Teilprojekts „Auswirkung der mechanischen Alterung von Beton auf das Tragverhalten von Massivbauteilen“ des DFG Graduiertenkollegs 2075 „Modelle für die Beschreibung der Zustandsänderung bei Alterung von Baustoffen und Tragwerken“ wurden am iBMB, Fachgebiet Massivbau der TU Braunschweig Untersuchungen zur Ermittlung der Schrägrisslast durchgeführt. In diesem Beitrag wird zunächst über die Ergebnisse an Stahlbetonbauteilen mit Rechteckquerschnitt ohne Querkraftbewehrung unter monoton steigender Belastung berichtet.

2 Rechnerische Ermittlung der Schrägrisslast

2.1 Allgemeines

Schrägrisse treten bei Querkraftbeanspruchung infolge der Überschreitung der effektiv nutzbaren Betonzugfestigkeit f_ct,ef auf. Hierbei kann zwischen Stegzugrissen und Biegeschubrissen unterschieden werden. Stegzugrisse stellen sich in zuvor ungerissenen Stegbereichen ein, wohingegen sich Biegeschubrisse aus vorhandenen Biegerissen entwickeln. Die zugehörige Schrägrisslast ist die Lastgröße, bei der der Stegzugriss sichtbar beziehungsweise der vorhandene Biegeriss einen schrägen Verlauf annimmt und zu einem Biegeschubriss wird.

Im Rahmen der Arbeiten wurde für die Ermittlung der Schrägrisslast auf folgende mechanisch begründete Ansätze zurückgegriffen:

• Ansatz nach technischer Biegetheorie (nachfolgend als B-Theorie bezeichnet)
• Ansatz nach Hong/Ha [8]
• Ansatz nach Gallego [9], [10]

Bei diesen Ansätzen werden auf Grundlage des Mohr‘schen Spannungskreises Hauptzugspannungen s₁ auf die effektiv nutzbare Betonzugfestigkeit f_ct,ef begrenzt

(1)

und die Schrägrisslast durch Integration der angenommenen Schubspannungsverteilung über die mitwirkende Querschnittshöhe h_ef (ungerissener Bereich) ermittelt:

(2)

2.2 Ansatz nach B-Theorie

Die technische Biegetheorie [11] setzt einen ungerissenen Querschnitt und ein linear elastisches Werkstoffverhalten voraus und hieraus ergibt sich die Schrägrisslast für biegebeanspruchten Bauteile zu:

(3)

Bei diesem Ansatz wird eine parabelförmige Schubspannungsverteilung und damit die Höhenlage der maximalen Schubspannungen h_l zu h/2 angenommen.

Für Bauteile mit Rechteckquerschnitt mit der Breite b und der Höhe h kann Gleichung (3) wie folgt vereinfacht werden:

(4)

Hierbei wird ein ungerissener Querschnitt beziehungsweise eine mitwirkende Querschnittshöhe h_ef entsprechend der Querschnittshöhe h vorausgesetzt.

2.3 Ansatz nach Hong/Ha

Nach Hong/Ha [8] kann die Schrägrisslast wie folgt ermittelt werden:

V_cr,cal = 0,56 · b · d · f_ct,ef (5)

Hierbei wird angenommen, dass der Querschnitt einen Biegeriss bis zur Biegezugbewehrung aufweist und damit die mitwirkende Querschnittshöhe h_ef der statischen Nutzhöhe d entspricht. Die maximale Schubspannung t_xz wird auf Höhe der statischen Nutzhöhe d angenommen (Bild 3). Damit wird eine mechanische Begründung des Ansatzes nach ACI 318–08 [12], Abschnitt 11.2.1 geliefert.

Der vollständige Beitrag ist erschienen in:

Bauingenieur 6.2018, Seite 248-254

Literatur

[1] BMVBS: Richtlinie zur Nachrechnung von Straßenbrücken im _Bestand (Nachrechnungsrichtlinie). Aus_gabe: 05/2011

[2] Hegger, J.; Maurer, R.; Zilch, K. Rombach, G.: Beurteilung der Querkraft- und Torsionstragfähigkeit von Brücken im Bestand – Kurzfristige Lösungsansätze. Schlussbericht für die Bundesanstalt für Straßenwesen, FE 15.0482/2009/FRB, Mai 2014.

[3] BMVI: 1. Ergänzung zur Richtlinie zur Nachrechnung von Straßenbrüc_ken im Bestand (Nachrechnungsrichtlinie). Ausgabe 04/201₅.

[4] Hegger, J.; Marzahn, G.; Teworte, F.; Herbrand, M.: Zur Anwendung des Hauptzugspannungskriteriums bei der Nachrechnung bestehender Spannbetonbrücken. In: Beton- und Stahlbetonbau 110 (2015), Heft 2, S. 82-95.

[5] Marzahn, G.; Hegger, J.; Maurer, R.; Zilch, K.; Dunkelberg, D.; Kolodziejczyk, A.; Teworte, F.: Die Nachrechnung von Bestandsbrücken – Fortschreibung der Nachrechnungsrichtlinie. In: Beton-Kalender 2015. Bauen im Bestand, Brücken, Ernst & Sohn, Berlin , 2015, S. 821-904.

[6] Huber, P.; Kromoser, B.; Huber, T.; Kollegger, J.: Berechnungsansatz zur Ermittlung der Schubtragfähigkeit bestehender Spannbetonbrückenträger mit geringem Querkraftbewehrungsgrad. In: Bauingenieur 91 (2016), Heft 6, S. 227-237.

[7] Fischer, O.; Müller, A.; Lechner, T.; Wild, M.; Kessner, K.: Ergebnisse und Erkenntnisse zu durchgeführten Nachrechnun_gen von Betonbrücken in Deutschland. In: Beton- und Stahlbetonbau 109 (2015), Heft 2, S_{. 107}-127.

[8] Hong, S. G; Ha, T.: Effective Capacity of Diagonal Strut for Shear Strength of Reinforced Concrete Beams without Shear Reinforcement. In: ACI Structural Journal, Vol. 109 (2012), Iss. 2, pp. 139–148.

[9] Gallego, J. M.: Shear fatigue behaviour of reinforced concrete elements without shear reinforcement. In: Müller, H. S.: Proceedings of the 9th fib symposium, 2012, pp. 17–22.

[10] Gallego, J.; Zanuy, C.; Albajar, L.: Shear fatigue behaviour of reinforced concrete elements without shear reinforcement. In: Engineering Structures, Vol. 79 (2014), S. 45–57.

[11] Schardt, R.: Verallgemeinerte Technische Biegetheorie – Lineare Probleme. Springer-Verlag Berlin Heidelberg, 1989.

[12] ACI Committee 318: Building Code Requirements for _Structural Concrete (ACI 318M-08), American Concrete Institute, 2008.

[13] Reineck, K. H.; Kuchma, D. A.; Fitik, B.: Erweiterte Datenbanken zur Überprüfung der Querkraftbemessung für Konstruktionsbetonteile mit und ohne Bügel. In: DAfStb-Heft 597, Beuth Verlag, 2012.

[14] Van den Berg, F. J.: Shear Strength of Beams without Web Reinforcement. Part 2 – Factors Affecting Load at Diagonal Cracking. In: ACI Journal, Vol. 59 (1962), Iss. 11, pp. 1587-1600.

[15] Marí, A.; Bairán, J.; Cladera, A.; Oller, E.; Ribas, C.: Shear-flexural strength mechanical model for design and assessment of reinforced concrete beams. In: Structure and Infrastructure Engineering, Vol. 11 (2015), Iss. 11, pp. 1399-1419.

[16] Hegger, J; Görtz, S.: Querkraftmodell für Bauteile aus Normalbeton und Hochleistungsbeton. In: Beton- und Stahlbetonbau 101 (2006), Heft 9, S. 695-705.

[17] Huber, P; Huber, T.; Kolleger, J.: Investigation of the shear crack behavior of RC beams on the basis of measured crack kinematics. In: Engineering Structures, Vol. 113 (2016), pp. 41-58.

[18] Krefeld, W. J.; Thurston, C. W.: Studies of the Shear and Diagonal Tension Strength of Simply Supported Concrete Beams. In: ACI Journal, Vol. 63 (1966), Iss. 4, pp. 451-476.

[19] Mathey, R. G.; Watstein, D.: Shear strength of beams without web reinforcement containing deformed bars of different yield strengths. In: ACI Journal, Vol. 60 (1963), Iss. 2, pp. 183-208.

[20] Xie, Y.; Ahmad, S. H.; Yu, T.; Hino, S.; Chung, W.: Shear Ductility of reinforced Concrete Beams of Normal and High-Strength Concrete. In: ACI Structural Journal, Vol. 2 (1994), pp. 140-149.

[21] Mphonde, A.G.; Frantz, G. C.: Shear tests of high-and low-strength concrete beams without stirrups. In: ACI Journal, Vol. 81 (1984), Iss. 4, pp. 350-357.

[22] Schacht, G.: Experimentelle Bewertung der _Schubtragsicherheit von Stahlbetonbauteil_en. Technische Universität Dresden, Dissertation, 2014.

_[23] Bažant, _Z. P.; _Kim, J.-K.: Size effect in shear failure of longitudinally reinforced beams. In: ACI Journal, Vol. 81 (1984), pp. 456-468.

[24] DIN EN 1992–1–1:2011–01 + DIN EN 1992–1–1/NA:2013–04: Euro_code 2 + Nationaler Anhang – National festgel_egte Parameter – Eurocode 2: Bemessung und Konstruktion von Stahlbe_ton- und Spannbetontragwerken – Teil 1–1: Allgemeine Bemessungsregeln und Regeln für den Hochbau.

[25] Zilch, K.; Zehetmaier, G.: Bemessung im konstruktiven Betonbau. Springer-Verlag Berlin Heidelberg, 2. neu bearb. u. erw. Aufl., 2010.

[26] Görtz, S.: Zum Schubrissverhalten von Stahlbeton- und Spannbetonbalken aus Normalbeton und Hochle_istungsbeton. RWTH Aachen, Dissertation, 2004.

[27] Kley, C.; Mark, P.: Zur Mindestquerkraftbewehrung von Stahlbetonbalken. In: Beton- und Stahlbetonbau 111 (2016), Heft 11, S. 728–737.

[28] Holz, K.: Untersuchu_ng der schrägen Rissentwicklung im Stahlbeton. Technische Universität Dresden, Institut für Massivbau, Projektarbeit, 2014.