Hybrid-Wärmespeicher mit Wasser und PCM-Granulat
In diesem Beitrag wird ein thermischer Energiespeicher (TES) auf Basis eines Phasenwechselmaterials (PCM) und Wasser mit einem Energieinhalt von 22 bis 27 kWh abhängig von der maximalen Speichertemperatur von 60 °C vorgestellt. Die Phasenwechselgrenze des PCM liegt bei einer Temperatur von 43 °C. Der Speicherinhalt besteht aus zwei Teilen: einem hochdynamischen Speicher von 400 l Wasser mit sensibler Wärme und einem eingeschränkt dynamischen Speicher von 300 kg PCM-Granulat mit sensibler und latenter Wärme.

PCM-Granulat mit mittleren Durchmessern von 2–5 mm. Bild: Goeke/Henne/Büttgen
Durch den Wasseranteil kann der Speicher sehr schnell be- und entladen werden. Durch den Phasenwechsel wird zusätzlich Wärmeenergie zeitlich verzögert aufgenommen. Neben der allgemeinen Funktionsweise des Speichers und der Vorgänge bei der latenten Wärmespeicherung interessiert besonders die Leistung des Speichers. Diese wird durch die Zeit-Ladefunktion Q(T,t), also die Abhängigkeit der Ladezeit von der wirksamen Temperaturdifferenz, repräsentiert. Darüber hinaus gibt die Austauschkapazität CA(T,t) Auskunft über die Leistungsfähigkeit und die Dynamik des Speichers. Die genannten Funktionen erlauben es, die Reaktion des Speichers auf schwankende Wärmeangebote zu beurteilen.
Der Speicher ist in ein Wärmeversorgungskonzept mit Wärmepumpe integriert. Die Wärmepumpe wiederum wird mit PV-Energie betrieben und die Luft in den eingesetzten PVT-Modulen vorgewärmt.
Einleitung
Thermische Hochleistungsspeicher im Gebäude werden in Zukunft immer wichtiger, weil sie das schwankende Angebot unterschiedlicher erneuerbarer Energie von Windstrom, Photovoltaik und Solarthermie sowie weiteren Erzeugern thermischer Energie ausgleichen müssen, denn die eigentliche Veränderung der Energieversorgung findet auf dem Wärmemarkt statt. Der Einsatz von Wasserspeichern ist zwar preiswert, aber in manchen Fällen nicht adäquat, wenn zum Beispiel bei der Sanierung von Gebäuden im Bestand beschränkte Platzverhältnisse herrschen. Hier wird die Wirkungsweise eines thermischen Energiespeichers für Wärme auf der Basis eines paraffinhaltigen Phasenwechselmaterials und Wasser vorgestellt. Im Mittelpunkt dieser Arbeit steht dabei insbesondere das Ladeverhalten und die zeitliche Temperaturentwicklung innerhalb des Speichers.
Anwendung des Phasenwechselmaterials
Der Einsatz von Phasenwechselmaterial (PCM) für die Energiespeicherung ist in den letzten zehn Jahren wieder stark in das Interesse der Wärme- und Kälteversorgung gerückt. Bei der Verwendung von thermischen Speichern im Gebäude sind für den Einsatz folgende Kriterien heranzuziehen: die Energiedichte im Speicher, die Einsatztemperatur und die Schmelztemperatur des PCMs. Die Speichertemperatur muss zum Einsatz passen, damit es durch die Temperaturunterschiede zwischen Anwendungstemperatur und Speichertemperatur nicht zu unnötigen Verlusten im System kommt. Für die Anwendung im Gebäude im Heizfall sollten die Temperaturen der Phasenwechsel zwischen 35 °C und 60 °C liegen, um optimale Wirkungsgrade mit den unterschiedlichen Wärmeerzeugern zu gewährleisten.
In wichtigen Übersichtsartikeln werden der Einsatz von PC-Materialien und die Verbesserungen in der Speichertechnik der letzten Jahre beschrieben. Dazu wurde in zahlreichen Studien immer wieder versucht, den Nachteil von PC-Materialien, die schlechte Wärmeleitung (l = 0,2 Wm-1K-1 bis l = 0,6 Wm-1K-1), durch unterschiedliche Maßnahmen zu kompensieren. Besonders zu erwähnen sind die Übersichtsartikel von Agyenim et al. [1], Pomianowskia et al. [2], Soares et. al. [3], Liu et. al. [4] sowie das Buch von Mehling und Cabeza [5]. Eigene Untersuchungen zur Funktionalität von Phasenwechselmaterialien und Wärmeübertragungssystemen [6–9] haben zur Auswahl dieses Speichertyps bestehend aus Phasenwechselmaterial und Wasser geführt. Cabeza et al. beschreiben das Speicherverhalten eines Wassertanks mit integrierten PCM-Modulen [10]. Brunkau et al. [11] untersuchten das Strömungsverhalten innerhalb der hier verwandten PCM-Granulatschüttung.
Theoretische Speicherfunktionsbeschreibung
Bei der Beschreibung der Speicherfunktionalität handelt es sich grundsätzlich um die Beschreibung des Wärmetransports von der äußeren Wärmequelle in den Speicher, der Beschreibung und des Wärmeübergangs auf das PCM und dem nachfolgenden Schmelz- oder Erstarrungsvorgang. Beide Vorgänge können komplementär betrachtet werden.
In dem hier vorgestellten Speicher mit Wasser- und PCM-Füllung hängt der energetische Füllzustand von dem Volumenstrom des im Wärmeerzeuger erwärmten Wassers und von der nachfolgenden Erwärmung des PCMs ab. Dabei ergänzen sich zwei unterschiedliche Lade- und Entladevorgänge im Speicher. Im Falle des Wassers wird der Speicher von unten nach oben mit warmen Wasser gefüllt. Damit steigt die Wärmeenergie für den Wasseranteil linear. Es besteht bei der Erwärmung keine Schichtung im klassischen Sinn, da sich kein Wärmeübertrager im Speicher befindet.
Von der Wärmeenergie des Wassers wird das PCM zuerst im sensiblen Bereich erwärmt, bis das Gebiet der Phasenwechseltemperaturen erreicht ist. Danach findet die Einlagerung von Wärme im Phasenwechsel statt. Die Gesamtwärmemenge setzt sich zusammen aus
Q(T,t) = QWasser, sensibel(t) +
+ QPCM, sensibel(t) + QPCM, latent(T,t) (1)
Im Fall des Wassers wird der Speicher in einer bestimmten Zeit gefüllt und es liegt ein linearer Anstieg der Wärmemenge im Speicher vor, bis die maximale Füllhöhe erreicht ist. Im Fall der sensiblen Wärmemenge des PCM liegt ein nichtlineares Verhalten vor, da dem Wasser Wärmeenergie für die Erwärmung des PC-Granulats entzogen wird. Ein nichtlineares Verhalten tritt dann während der Schmelzphase des PC-Granulats auf. Es wird durch die Peclet-Gleichung beschrieben [6, 7]. Da der Anteil der sensiblen Wärmemenge des PCMs je nach Temperaturgrenzen maximal 9 % beträgt, ist der Einfluss der Nichtlinearität in Bezug auf die Speicherbeladung gering. Den größten Einfluss auf die Speicherladefunktion Q(t) hat die Phasenumwandlung des PCMs. In diesem Fall gibt das Wasser Wärme an das Granulat ab und wenn die Schmelztemperatur erreicht ist, beginnt die Umwandlung. Dieser Vorgang findet zeitverzögert statt, da die Speicherbeladung ungefähr bei 25 °C beginnt und bei 40 °C die erste Phasenumwandlung stattfindet. Eine Wärmeteilmenge des Wassers dQ wird an ein- zelne PCM Körner übertragen. Parallel nimmt bei diesem Prozess die Temperatur des Wassers um den Betrag DT ab. Aufgrund des direkten Wärmetransports durch das Wasser auf eine große PCM-Granulatoberfläche liegt ein guter Wärmeübergang vor.
Latente Wärme des PCM und zeitabhängige Phasenumwandlung
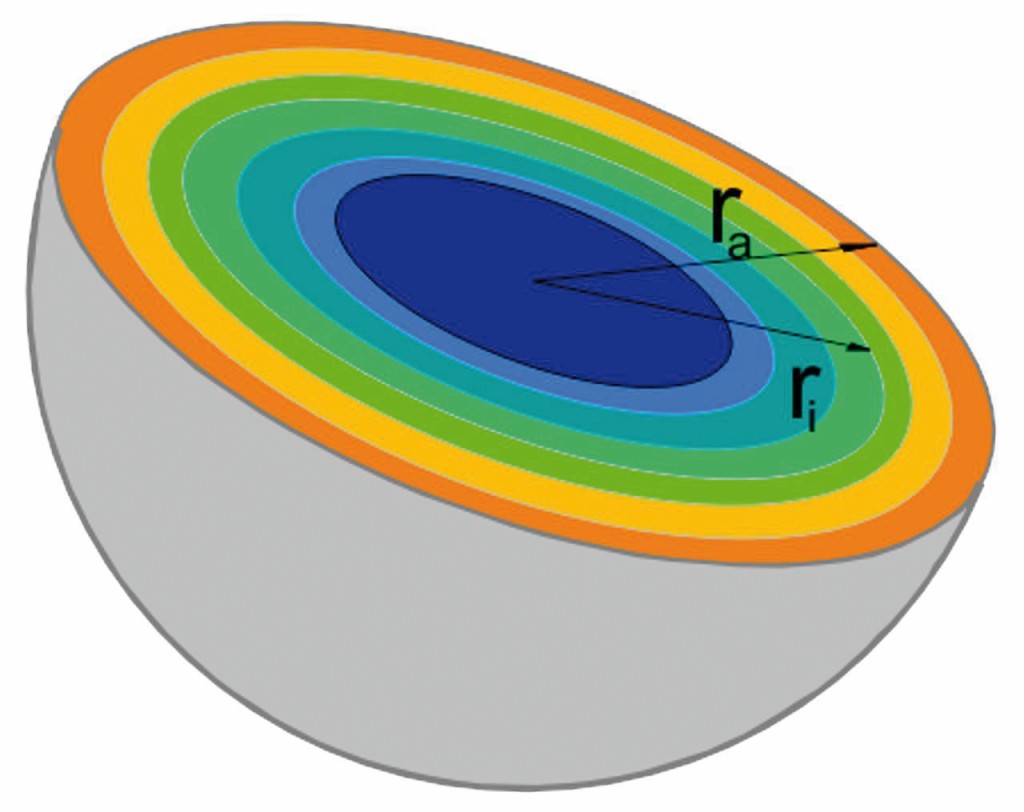
Die Zunahme des Wärmeinhalts des PCM-Granulats lässt sich mit Methoden der klassischen Thermodynamik beschreiben, wenn das einzelne Granulatkorn in einer Näherung als Kugel betrachtet wird. Für den Wärmeübergang ist die wirksame Oberfläche wichtig, sie beträgt 0,8 m²/l. Damit kommt man auf eine kalkulatorische Gesamtoberfläche von 220 m². Diese Fläche ist jedoch thermodynamisch nicht voll wirksam. Versuche haben gezeigt, dass die Hälfte der geometrischen Fläche als thermodynamisch wirksame Fläche angesehen werden kann, denn durch die kompakte gegenseitige Anlagerung, ist der strömungstechnische Wärmetransport behindert.
Das obenstehende Bild zeigt die langsame Erwärmung des PCM Granulats, angedeutet durch unterschiedliche Farbringe. In einer bestimmten Zeit wird eine Wärmemenge dQ vom äußeren Radius ra bis zum Radius ri in die Kugel eindringen. Dies geht einher mit einem Temperaturabfall von der Oberfläche bis ins Innere der Kugel.
Die Berechnung der Schmelzzeit erfolgt mit einer Anpassung der Pecletgleichung für eine Vollkugel1). Bei dieser Betrachtung wird davon ausgegangen, dass sich die Granulatkugel in einem nicht bewegten Wasserbad mit konstanter Temperatur oberhalb der Schmelztemperatur befindet.
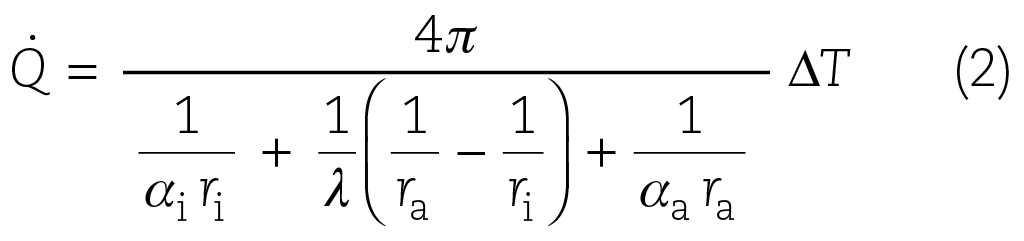
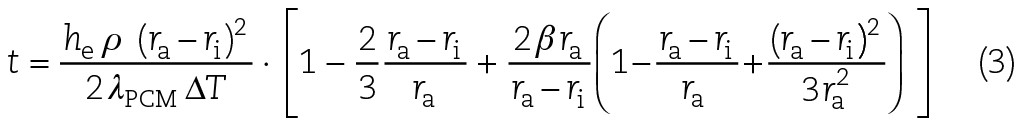
Dabei ist he die Schmelzenthalpie, lPCM die Wärmeleitfähigkeit, rPCM die Dichte und DT die Temperaturdifferenz. Im Falle der Erwärmung wird der Radius ri gegen den maximalen Radius der Kugel ra laufen. lW ist die Wärmeleitfähigkeit der Wand bei Rohrwärmeübertragern.
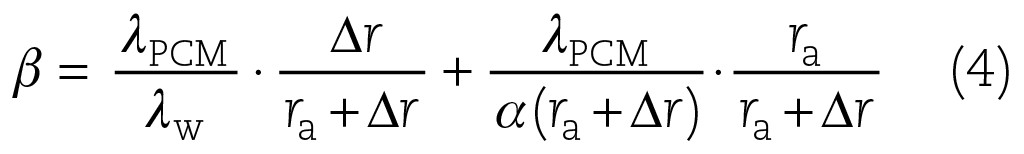
Da keine Rohrwandung vorhanden ist, beziehungsweise eine zu vernachlässigende Wassergrenzschicht, wird Dr zu Null und man erhält

Zur Berechnung der Wärmemenge Q(t) lässt sich einerseits eine Summation kleiner Änderungen des Radius ri durchführen und die in der Zeit aufgenommene Wärme Qi(ti, ti+1) berechnen [6]. Andererseits lässt sich die maximale Zeit mit ri = 0 als reziproke Zeitkonstante in die Gleichung einer Blockkapazität einsetzen. Bildet man den Grenzwert mit ri–>0, so wird Gl. (3)
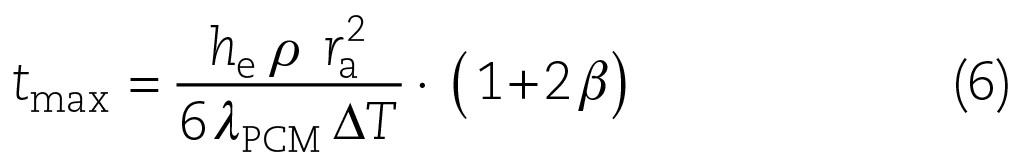
Die Gleichung für tmax sieht dann folgendermaßen aus:
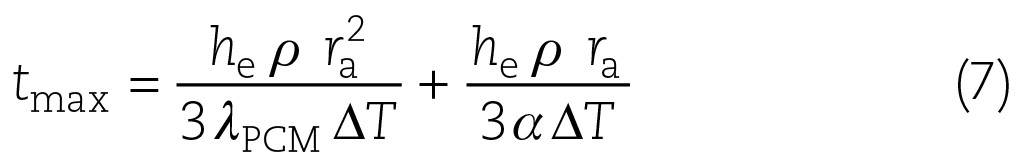
Der quadratische Anteil in tmax ist vernachlässigbar. Dann kann man in guter Näherung schreiben:

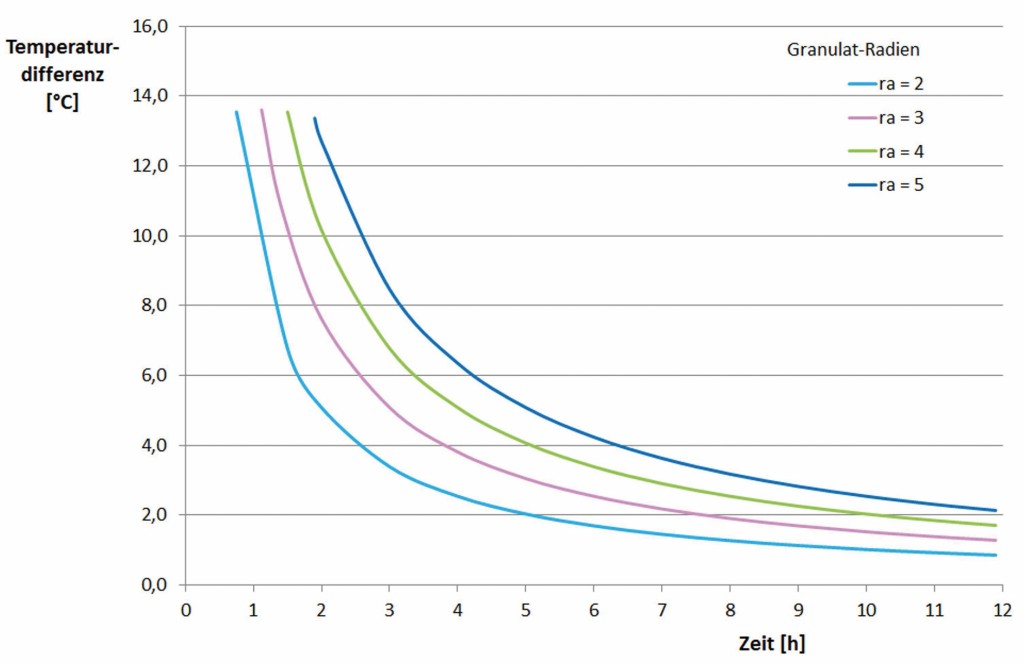
Das Ergebnis dieser Betrachtung ist der Verlauf der maximalen Schmelzzeit. Sie ist im nachfolgenden Bild dargestellt.
Die Ergebnisse sind für die Radien 2,3,4,5 mm berechnet. Wobei das Maximum der Radien des Granulats bei 2,5 mm ±0,5 mm liegt.
In der Abbildung ist die maximale Schmelzzeit während des Phasenwechsels in Abhängigkeit der einzelnen Korngrößen und der Temperaturdifferenz aufgetragen. Dabei gelten diese Schmelzzeiten nur für eine einzelne, gleichmäßig umströmte Kugel. In einer stochastischen Schüttung wie bei dem eingesetzten PCM-Granulat ist nur eine Teilumströmung gegeben, so dass die Schmelzzeiten sich vergrößern können.
Damit lässt sich der zeitliche Verlauf der Energieaufnahme im latenten Bereich des Speichers, also für das PCM-Granulat, angeben. Wird der allgemeine Ansatz mit Hilfe der e-Funktion gewählt, so lautet die Gleichung
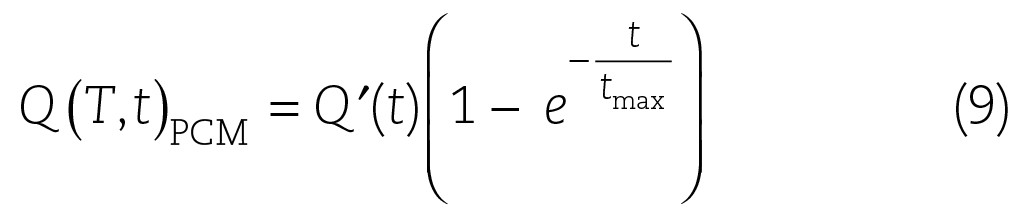
Damit lässt sich für jede Temperaturdifferenz DT, der Differenz der Radien ra und ri und den bekannten Parametern aus der Pecletgleichung die Zeit und daraus den Ladezustand des Speichers berechnen. Der Nachteil dieses Vorgehens liegt in der expliziten Einbeziehung der Radien bzw. des Schmelzzustandes des Granulats. Daher wird alternativ ein Lösungsansatz über die Einbeziehung der Leistung vorgeschlagen.
Zeitabhängigkeit der Ladefunktion des PCM im Speicher
Die Zeitkonstante zur Beladung wie auch Entladung eines thermischen Speichers muss durch die Definition der Gesamtenergie des Speichers bestehend aus den Teilenergien erfolgen. Diese wird auf die Leistung bezogen. Dadurch wird eine Zeitkonstante für den gesamten Lade- wie Entladevorgang des thermischen Speichers bestimmt. Hier wird sie Speicherladekennzahl genannt. Sie lautet
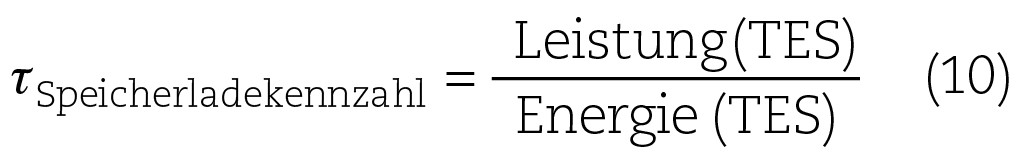
Es ist die Zeitkonstante, welche eine ideale exponentielle Beladungskurve beschreibt, wenn die thermodynamische Beladungsfunktion eine ideale Sprungfunktion darstellt und die Leistung konstant bleibt. Die Wärmeübertragung dQ ist dabei proportional der insgesamt zur Verfügung stehenden bzw. aufzunehmenden Wärmemenge, wobei Q selbst wiederum linear wächst. Dann kann man schreiben
dQ = Q(t) t(t) (11)
Der thermodynamische Widerstand und die spezifischen Wärmekapazitäten im sensiblen wie im latenten Bereich bestimmen den zeitlichen Verlauf der Be- und Entladung. Die Energie des Speichers ist in der Hauptsache im latenten Anteil Dhlatent des PCMs und dem sensiblen Anteil Qsensibel des Wassers enthalten. Der sensible Anteil des PCMs liefert den bereits bekannten Beitrag von ~9 %. Die Leistung wird bestimmt durch die Wärmeübergangszahl a, die aktive Wärmetauscherfläche A und die Temperaturdifferenz DT. Damit ist die Zeitkonstante eine, wie man bereits bei den einzelnen Granulatkörnern gesehen hat, temperaturabhängige Größe. Die Ladekennzahl lautet
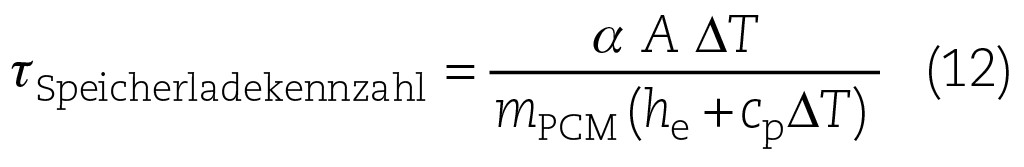
Die Aufladung eines thermischen Speichers kann dann durch Integration der Gl. (11) oder durch die Anwendung der Laplace-Transformation erfolgen. Allerdings ist zu berücksichtigen, dass die Wärmemenge Q des in den Speicher eintretenden warmen Wassers sich verändert, so dass sich auch das thermodynamische Potential DT zeitlich ändert. Dieser Vorgang muss durch eine zeitliche Abhängigkeit der Wärmemenge des warmen Wassers QH2O (t) berücksichtigt werden.
Der zeitliche Verlauf der Wärmemenge des PCMs kann dann wie folgt geschrieben werden:
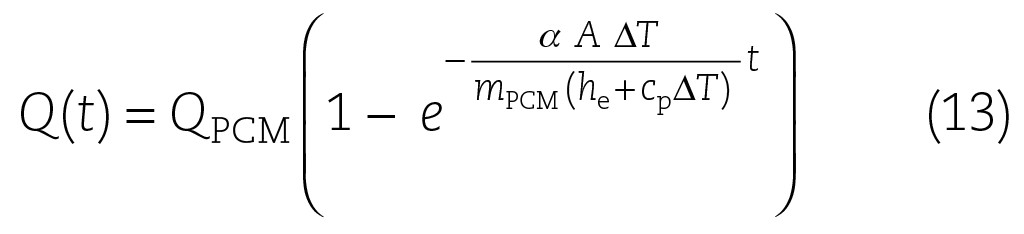
Der Wärmeübergangskoeffizient a wird über die Nusseltzahl und die mittlere freie Weglänge bestimmt. Als Nusseltzahl für die laminare sehr langsame Strömung wurde ein Nu = 3,66 und eine mittlere freie Weglänge aus Behälterdurchmesser und planarer Flächendichte durch Kreisscheiben von D = 0,17 m ermittelt. Damit erhält man einen Wärmeübergangskoeffizienten a von ~8. Die empirisch ermittelte wirksame thermodynamische Fläche beträgt ~110 m². Mit dieser Tatsache lässt sich ein Reduktionsfaktor in Zukunft beschreiben.
Zeitabhängigkeit der Ladefunktion des Wasser im Speicher
Zu der Wärmemenge, die das PCM aufnehmen kann, kommt noch die Wärmemenge, die das Wassers aufnimmt. Dabei wird der Speicher langsam mit einer Geschwindigkeit von ungefähr 1 mm/s gefüllt. Dies entspricht einer linearen Funktion für die Wärmemenge Q in Abhängigkeit vom Volumenstrom bei einem gleichbleibenden Behälterquerschnitt.

Die Wärmeenergie wird dann nach Kontakt mit dem PCM-Granulat teilweise von diesem aufgenommen, so dass die lineare Funktion Gl. (14) um einen Term erweitert werden muss, der am Ende des Vorgangs sich asymptotisch an den Endzustand der Wärmemenge annähert und die Wärmeabgabe des Wassers an das PCM-Granulat beschreibt. Somit wird die Gl. (14) in erster Näherung um einen quadratischen Term erweitert:
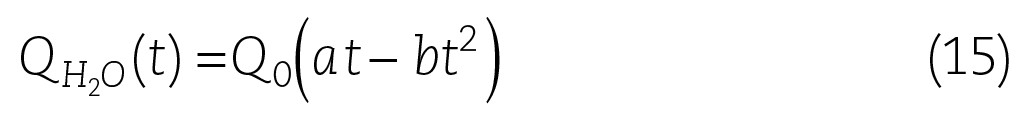
Der Proportionalitätsfaktor a wird neben dem Füllvolumen des Speichers ebenso durch die Leistung des äußeren Wärmeversorgers bestimmt. Der Wärmeübergang vom Wasser auf das PCM-Granulat, der eine zeitlich verzögerte anschließende Phasenumwandlung auslöst, wird in 1. Näherung durch den Parameter b repräsentiert. Dieser Wärmetransport und Umwandlungsprozess bestimmt, ob die bereitgestellte solare Energie auch in der vorgesehenen Zeit im Speicher untergebracht werden kann oder ob nur ein Teil dieser Energie eingelagert werden kann. Eine mathematisch-physikalische Lösung muss die Wechselwirkung zwischen dem warmen Wasser (Vorlauf), der dann folgenden Wärmeabgabe an das PCM-Granulat und dem Anteil des verbleibenden warmen Wassers im Speicher beschreiben.
Als Gesamtladefunktion für den Speicher erhält man als Resultat der Wärmeenergie im Wasser und im PCM-Granulat 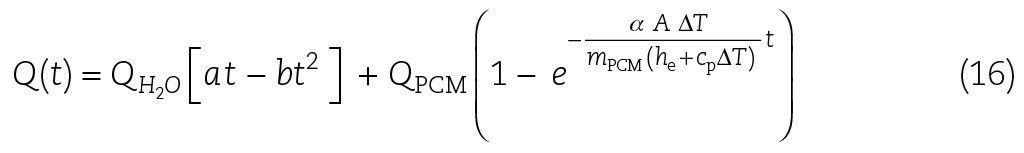
Da die gesamte Wärmeenergie durch das Wasser in den Speicher transportiert werden muss, bekommt der Koeffizient a eine entsprechende Definition. Damit ist a der Quotient aus Gesamtenergie/Gesamtzeit. Der Koeffizient b ist somit der Quotient aus Gesamtenergie/Gesamtzeit zum Quadrat.
Eine mathematische-analytische Lösung und eine Simulation mit Fluent sind zurzeit in Bearbeitung. Die aus diesen theoretischen Überlegungen gewonnene Ladefunktion wird bei der Diskussion der Messergebnisse mit diesen verglichen.
Speicherdynamik und Austauschkapazität
Neben dem Verlauf der Wärmemenge im Speicher ist es, wie bereits erwähnt, wichtig, die Dynamik des Speichers zu beschreiben. Dies gilt insbesondere dann, wenn ein bestimmtes Speichersystem und eine Bauart unter konkurrierenden Systemen ausgewählt werden soll. Dazu wird hier eine Austauschkapazität CA eingeführt, die es ermöglicht die Dynamik eines Speichers zu beurteilen. Dazu bedient man sich der Definition der Entropie. Das Verhältnis der Temperatur einerseits im Vorlauf und Rücklauf andererseits im Speichermaterial bezogen auf die Änderung der Wärmemenge dQ im Speicher ist Ausgangspunkt der Definition. Sie lautet bezogen auf die Entropie als irreversibler Anteil,
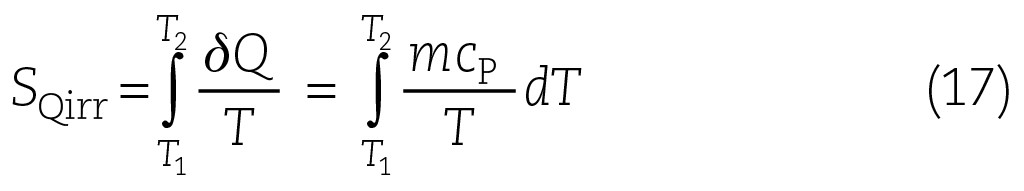
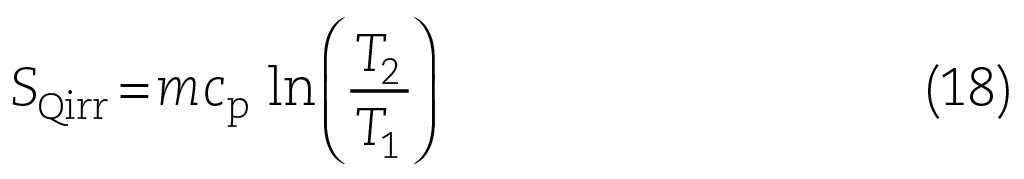
Die Temperatur T2 wird durch die Temperaturdifferenz von Vorlauf und Rücklauf bestimmt. Die Temperatur T1 wird durch die Temperatur TSP im Speicher und der Vorlauftemperatur TVL bestimmt. Damit erhält man folgenden Ausdruck:
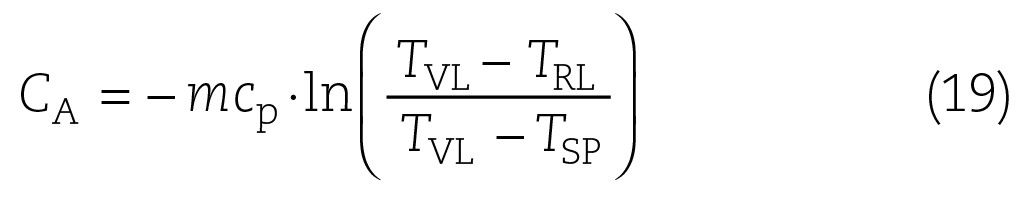
In der Regel bleibt das Argument des natürlichen Logarithmus zwischen null und eins und damit negativ. Das negative Vorzeichen dient allein der Umkehrung also der positiven Darstellung zur besseren Lesbarkeit der Funktion. Bei der Be- und bei der Entladung tauschen die Temperaturen TVL/TRL und TVL/TSP die Plätze, so dass der Bruch immer positiv bleibt. Werden reale Messwerte in Gl. (19) eingesetzt, so sollte die Auswertung auf Temperaturdifferenzen oberhalb von 0,3 K begrenzt werden, da die Schwankungen durch Messunsicherheiten negative Argumente des Logarithmus zur Folge haben können.
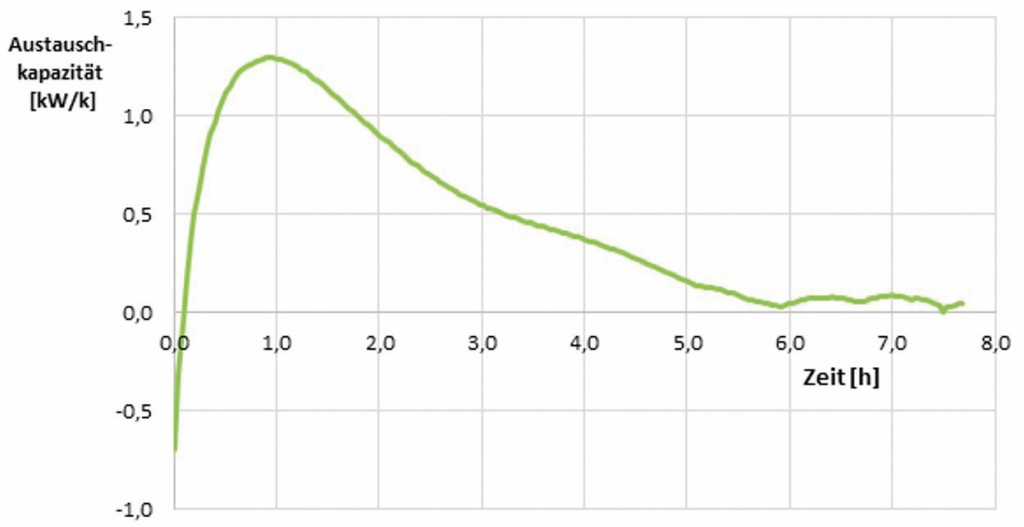
Im Bild ist die Beladephase des Speichers und seine dazu gehörende Austauschkapazitätsfunktion CA zu sehen.
Die Austauschkapazität beginnt im negativen Bereich, weil aufgrund der Anfangstemperaturen eine Wärmeabgabe entsteht. Er zeigt die Wärmezufuhr bereits zu Beginn der Beladung. Danach kommt es zu einem Maximum mit 1,3 kW/K. Wird die Temperaturdifferenz von 5 K herangezogen, so bedeutet dies eine Leistung von 6,5 kW, welche in den Speicher geladen werden kann. Am Ende der Beladung bestimmen Systemverluste und Schwankungen der Vorlauftemperatur die Funktion.
1) H. D. Bähr & K. Stephan, Wärme- und Stoffübertragung, Springer.
Literatur:
[1] Agyenim, F., Hewitt, N., Eames, P., Smyth, M:. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS), Renewable and Sustainable Energy Reviews 14 (2010) 615–628.
[2] Pomianowskia, M., Heiselberg, P., Zhang, Y.: Review of thermal energy storage technologies based on PCM application in buildings, Energy and Buildings 67 (2013) 56–69.
[3] Soares, N., Costab, J.J., Gasparb ,A.R., Santosc, P.: Review of passive PCM latent heat thermal energy storage systems towards buildings’ energy efficiency, Energy and Buildings 59 (2013) 82–103.
[4] Liu, M., Saman, W., Bruno, F.: Review on storage materials and thermal performance enhancement techniques for high temperature phase change thermal storage systems, Renewable and Sustainable Energy Reviews 16 (2012) 2118– 2132.
[5] Mehling, H., Cabeza, L.F.: Heat and cold storage with PCM: An up to date introduction into basics and applications, Springer, Berlin (2008).
[6] Goeke, J., Henne, A.: Speicherdynamik von Kälte-Speichern mit PCM-Compound Materialfüllung. HLH Bd. 64 (2013) Nr. 2, S. 21–27.
[7] Goeke, J., Ruhbach, K., Henne, A., Orth, D.: Messung der Phasenfrontgeschwindigkeit und der Energiespeicherung von PCM-Compoundmaterialien. HLH Bd. 61 (2010) Nr. 1, S. 49–53.
[8] Goeke, J., Henne, A.: Time-Temperature Charge Function of a High Dynamic Thermal Heat Storage with Phase Change Material, Energy and Power Engineering, EPE 7, (2015), 41–54, dx.doi.org/10.4236/epe.2015.72004
[9] Goeke, J., Otten, B.: Vergleich der konstruktiven Speichertechnik von PCM Wärme-Speichern. HLH Bd. 66 (2015) Nr. 3, S. 29-35.
[10] Cabeza, L.F., Ibánez, M., Solé, Ch., Roca, J., Nogués, M.: Experimentation with a water tank including, a PCM module, Solar Energy Materials & Solar Cells 90 (2006) 1273–1282.
[11] Brunkau, R., Kawasaki, Y., Herzog, E:. Wärmetechnisches Verhalten von Latentwärmespeichermaterial. HLH Bd. 66 (2015) Nr. 10, S. 18–22.
Prof. Dr. Johannes Goeke, Jahrgang 1953, Studium der Nachrichtentechnik an der FH Dortmund und Studium der Physik an der Universität Münster. Er vertritt an der Technischen Hochschule Köln im Institut für Technische Gebäudeausrüstung seit 1994 die Lehrgebiete Physik, Automatisierungstechnik, Signalverarbeitung und Sensortechnik. Arbeitsgebiete zurzeit, Thermodynamik der Wärme- und Kältespeicher mit Phasenwechselmaterial sowie deren Systemintegration.Prof. Dr. Andreas Henne, Jahrgang 1964 ist an der Technischen Hochschule Köln im Institut für Technische Gebäudeausrüstung Professor für Klima- und Kältetechnik sowie für das Fach Wärmeübertragung. Sein Arbeitsgebiet liegt insbesondere in der Energieeffizienz von Klima-/Kälteanlagen mit dem aktuellen F&E-Schwerpunkt Entwicklung und Einsatz von Latentwärmespeichern.Pascal Büttgen B.Eng., Jahrgang 1986, Studium der Energie- und Gebäudetechnik, Studienrichtung Technische Gebäudeausrüstung an der Technischen Hochschule Köln. Seit September 2015 Masterstudium Green Building Engineering und wissenschaftliche Hilfskraft am Institut für Technische Gebäudeausrüstung an der TH Köln.