Berechnung des Kreuzstrom-Plattenwärmeübertragers in der RLT

Für die Berechnung von Wärmeübertragern gibt es verschiedene Methoden, die sich bezüglich Aufwand, Genauigkeit und Anwendung unterscheiden. Meist ist es ausreichend, das Konzept der mittleren Temperaturdifferenz auf den gesamten Tauscher anzuwenden; es führt mit einfachen Formeln und Diagrammen schnell und ausreichend genau zum Ergebnis. Dazu sind einige idealisierte Annahmen, auch zur Stromführung, zu treffen [2]. Es gelten folgende Randbedingungen:

• stationäre Strömung
• feste Trennwände
• adiabates System
• keine Phasenänderung
• konstanter Druck
• konstanter Massenstrom
• keine Wärmeleitung/Mischung
• in Strömungsrichtung
• idealisierte Strömung
• kein Randeffekt

Bezüglich der Wärmerückgewinnung erleichtern folgende Definitionen die Berechnung:

• gleiches Medium bei beiden Strömen
• (Luft)
• gleicher Massenstrom bei beiden
• Strömen
• gleicher Wärmekapazitätsstrom bei
• beiden Strömen

Unter diesen Bedingungen berechnet sich die dimensionslose Temperaturänderung f (= Temperaturänderungsgrad = Rückwärmzahl) wie folgt:

 

 

 

Dabei sind:

1. Index:

1 Warmer Strom

2 Kalter Strom

m  mittlere Temperatur

2. Index:

1 Eintritt

2 Austritt

 

 

 

t   Temperatur

N Number of Transfer Units (Bei gegebenem Fluid wird dadurch die Mächtigkeit bzw. die Größe eines Übertragers ausgedrückt.)

 

 

 

k   Wärmeübergangskoeffizient

A  Übertragungsfläche

c_p  spezifische Wärmekapazität

m Massenstrom

Die bisherigen Ableitungen können mit einem Korrekturfaktor F sozusagen auf den Gegenströmer normiert werden.

 

 

Dt_m    mittlere Temperaturdifferenz

Dt_mG mittlere Temperaturdifferenz eines Gegenströmers

Damit erhält man die allgemein gültigen Formeln für alle Stromführungen

 

 

 

Der Korrekturfaktor F hängt von der Stromführung und von N ab:

 

 

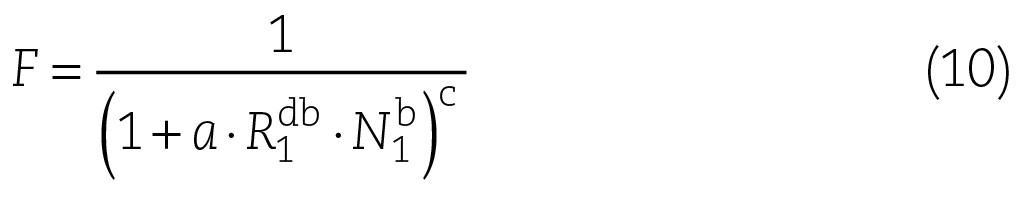
Der Korrekturfaktor F für einen Gegenströmer ist – gemäß Definition – 1,0. Die Faktoren a, b, c und d hängen von der Stromführung ab und sind beispielsweise in Tabelle 2 des VDI-Wärmeatlas aufgeführt [2].

Berechnung des Kreuzstrom-Wärmeübertragers

Mit Gl. (10) können die Korrekturfaktoren der verschiedenen Stromführungen berechnet werden. In der folgenden Tabelle sind einige Beispiele für die Faktoren a, b, c und d [3] aufgeführt.

Reiner Kreuzstrom

Das ist sozusagen die „natürliche“ Stromführung beim Kreuzstrom-Plattenwärmeübertrager in der Raumlufttechnik; beide Ströme weisen am Austritt quer zur Strömung unterschiedliche Temperaturen auf −> sie sind nicht quervermischt.

Einseitig und beidseitig quervermischt

Zunächst ist zu definieren, was „quervermischt“ bedeutet. Dazu ein Zitat: „Eine Quervermischung äußert sich durch eine einheitliche Temperatur. Das sich dann im jeweiligen Fluid ergebende Temperaturprofil ist eindimensional“ [3]. Der Temperaturgradient in Querrichtung ist also Null. Zur Quervermischung wären beim Kreuzstrom-Plattenwärmeübertrager in einem (einseitig) oder in beiden (beidseitig) Strömen zusätzliche Einbauten nötig.

Beurteilung und Stand der Technik

Kreuzstrom-Plattenwärmeübertrager in der Raumlufttechnik werden immer nach dem Prinzip des reinen Kreuzstroms durchströmt; es gibt weder ein- noch beidseitige Quervermischung. Dies wird durch die VDI-Richtlinie 3805 Bl. 5 bestätigt: „Die Temperaturverteilung nach dem Kreuzstrom-Plattenwärmeübertrager ist inhomogen.“

Stand der Technik ist somit, dass Kreuzstrom-Plattenwärmeübertrager als reine Kreuzströmer berechnet werden. Beweis für die Richtigkeit dieser Aussage sind die vielen Messungen, die z. B. Eurovent im Rahmen der Zertifizierung von Plattenwärmeübertragern in auditierten Prüflabors durchführen ließ. Sie belegen die Berechnungen mit reinem Kreuzstrom und bestätigen Werte, die weit über denen eines beidseitig quervermischten Kreuzströmers liegen [4].

Es gibt mehrere Gründe, keine quervermischten Plattenübertrager in der Raumlufttechnik einzusetzen. Die notwendigen Einbauten erhöhen Druckverlust und Kosten, der Temperaturänderungsgrad wird im Vergleich zum reinen Kreuzströmer aber reduziert. So sind mit dem beidseitig quervermischten Übertrager maximal nur knapp 57 % erreichbar. (Siehe dazu auch Bilder 30, 31 und 32 im VDI-Wärmeatlas [2].) Umso erstaunlicher ist es, dass in einigen Publikationen [1, 5, 6] der beidseitig quervermischte Kreuzstromübertrager als Referenz verwendet wird.

Berechnung des reinen Platten-Kreuzstromwärmeübertragers

Mit den Gln. (9) und (10) kann iterativ der Temperaturänderungsgrad f in Abhängigkeit von N berechnet werden. Die für die Berechnung von F notwendigen Faktoren sind dabei

a = 0,433

b = 1,600

c = 0,267

d = 0,5 (nicht relevant)

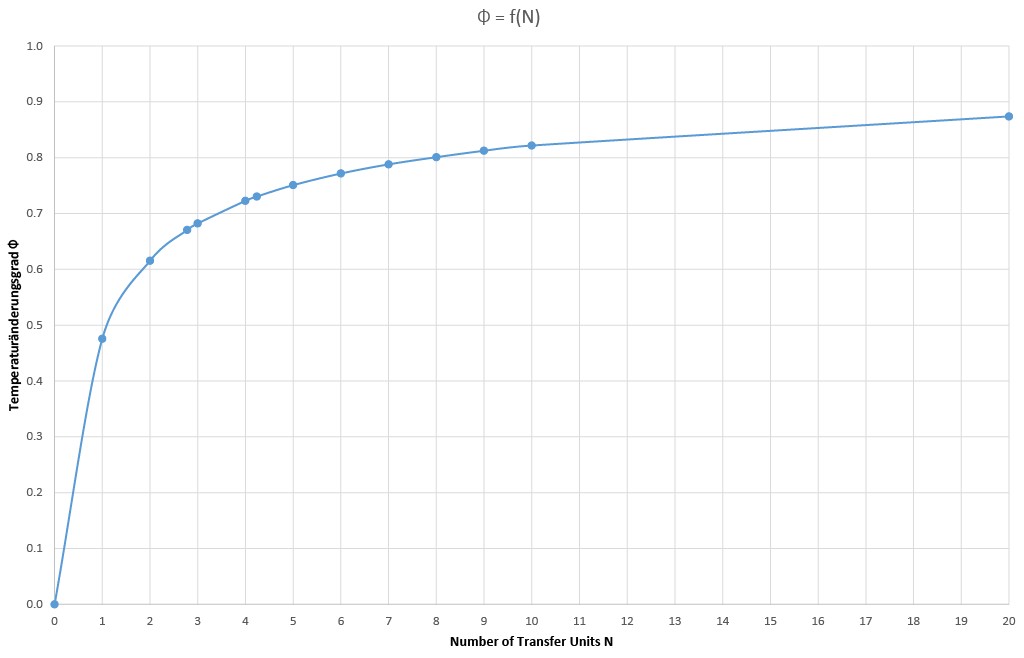
Das Ergebnis ist im folgenden Bild zusammengefasst.

• Mit steigendem N wird der Tempe- raturänderungsgrad (= Rückwärmzahl) höher. Je größer der Übertrager und je besser der Wärmeübergang desto höher ist die Effizienz. Mit N = ∞ erhält man einen Wert nahe 1,0.
• Der in der Ökodesign-Richtlinie ab dem 1.1.2016 vorgegebene Wert von 67 % wird mit N = 2,78 erreicht.
• Der in der Ökodesign-Richtlinie ab dem 1.1.2018 vorgegebene Wert von 73 % wird mit N = 4,24 erreicht.
• Die Zielwerte liegen in einem Effizienzbereich, der bereits heute mit Kreuzstrom-Plattenwärmeübertragern abgedeckt wird [4].

Laut [2] ist mit folgenden Toleranzen für den Temperaturänderungsgrad bei der Methode der mittleren Temperaturdifferenz zu rechnen:

f ≤ 0,7   2 %

f > 0,7   3 %

Dies kann man mit der hier möglichen, auf einer Arbeit von W. Nusselt basierenden [7] analytischen Lösung bestätigen.

 

 

 

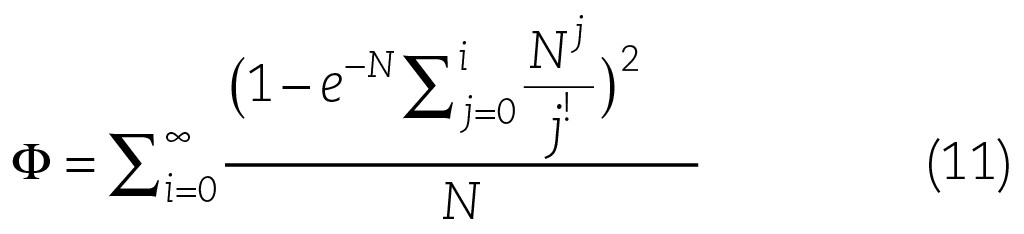
Für konkrete N-Werte erhält man die in der untenstehenden Tabelle aufgeführten Ergebnisse.

Ausblick

Die Hersteller von Kreuzstrom-Plattenwärmeübertrager können den neuen Vorgaben aus dem Ökodesign gelassen entgegen sehen. Die geforderten Werte werden bereits mit heutigen Übertragern erreicht, ja sogar übertroffen. Es ist zu erwarten, dass in Zukunft die Temperaturänderungsgrade weiter ansteigen werden. Die Berechnung als reiner Kreuzströmer zeigt auf, was möglich ist.

 

 

Literatur:

[1] Kaup, Ch.: Die neue Ökodesign-Richtlinie der EU, HLH Bd. 66 (2015) Nr. 2, S. 34-38.

[2] Roetzel, W. und Spang, B.: Berechnung von Wärmeübertragern, VDI Wärmeatlas 10. Auflage, Springer-Verlag, Berlin Heidelberg 2006.

[3] Heidemann, W.: Berechnung von Wärmeübertragern, Institut für Thermodynamik und Wärmetechnik, Vorlesung an der Universität Stuttgart 2015.

[4] Cherré, N.: Certified recovery systems and impact of the ecodesign regulation, Informationsblatt der Eurovent-Certification, Paris,

[5] Stahl, M. und Kaup, Ch.: Für Platten-WRG wird’s eng, CCI 3/2015, CCI Dialog Karlsruhe.

[6] Kaup, Ch.: Wärmerückgewinnung, Recknagel, Sprenger, Albers: Taschenbuch für Heizung und Klimatechnik, Band 2, S. 1518 ff, Deutscher Industrieverlag München 2015/2016.

[7] Nusselt, W.: Eine neue Formel für den Wärmeübergang im Kreuzstrom, VDI Zeitschrift Bd. 55 (1911) S. 2021.