Auf die Form kommt es an
Die Mikrogeometrie der Zahnflanke hat entscheidenden Einfluss auf die Tragfähigkeit einer Stirnradverzahnung. Mithilfe von Zahnflankenkorrekturen kann diese beeinflusst werden. Ziel der Korrekturauslegung ist es, die bestmögliche Kombination aus einer Vielzahl von Standardkorrekturarten und -formen zu ermitteln. Doch erst unter Berücksichtigung der Fertigung kann eine technisch und wirtschaftlich sinnvolle Zahnflankenmodifikation ausgelegt werden. Unter Berücksichtigung aktueller Weiterentwicklungen im Bereich des Verzahnungswälzschleifens werden im Folgenden neue Korrekturkombinationen hinsichtlich ihres Aufwands (Fertigungszeit) und Nutzens (Pressungsverteilung) für die Praxis bewertet.
![Bild 1 Einteilung der Standardkorrekturarten für evolventische Stirnräder nach DIN ISO 21771 aus [2]. Bild: Verfasser](https://www.ingenieur.de/wp-content/uploads/2020/01/KA-814-Bansemir-Geiser-Bild1-neu-980x574.jpg)
Bild 1 Einteilung der Standardkorrekturarten für evolventische Stirnräder nach DIN ISO 21771 aus [2]. Bild: Verfasser
Einleitung und Problemstellung
Zahnradgetriebe sind die am häufigsten verwendete Getriebeart. Sie finden in allen Größen- und Leistungsbereichen ihren Einsatz, vom Uhrwerk bis zur Windkraftanlage.
Die Leistung eines Zahnradgetriebes wird über den Zahnkontakt übertragen. Eine gleichmäßige Belastung auf der Zahnflanke soll eine gleichmäßige Werkstoffausnutzung und so die maximale Tragfähigkeit ergeben. Verformungen im gesamten Getriebe unter Last und Abweichungen, zum Beispiel aus der Fertigung, verursachen eine ungleichmäßige Belastungsverteilung auf der Flanke mit Lastüberhöhungen und zumeist eine geringere Tragfähigkeit. Durch Modifikation der Mikrogeometrie der Zahnflanke soll eine weitgehend gleichmäßige Belastungsverteilung auf der Zahnflanke für die Auslegungslast erzielt werden. Die Modifikationen werden als Zahnflankenkorrekturen in Profil- und Breitenrichtung beschrieben und mit den Angaben zu Korrekturbetrag, -länge und -form definiert.
Es gibt theoretisch unbegrenzt viele Kombinationsmöglichkeiten von Standardkorrekturen. Neben der händischen Korrekturanpassung und Auswahl, können beispielsweise Optimierungsverfahren wie nach [1] verwendet werden. Es können dabei verschiedene Korrekturziele verfolgt werden, zum Beispiel hinsichtlich maximaler Tragfähigkeit, minimalem Anregungsverhalten [7], [11], oder Berücksichtigung von Fertigungsabweichungen [4]. Jedoch wird die Auswahl durch die Herstellung der Korrekturen und die Kosten durch eventuelle zusätzliche Fertigungszeit eingeschränkt. Der Konstrukteur steht bei jeder Verzahnungsauslegung vor der Aufgabe, eine sowohl technische als auch wirtschaftlich sinnvolle Zahnflankenmodifikation festzulegen.
Aktuelle Weiterentwicklungen im Fertigungsprozess können diese Einschränkungen aufweiten und so das Verhältnis von Nutzen zu Aufwand verändern. Korrekturarten und -formen, die bisher für die Serienfertigung ungeeignet waren, können heute zu sinnvollen Lösungen führen.
Im Rahmen eines Forschungs-Projektes mit der Firma Liebherr Verzahntechnik wurden dazu exemplarisch Beispielauslegungen und -berechnungen durchgeführt. Mit der Verbindung von Fertigungs- und Berechnungskompetenz sollten neue Korrekturkombinationen hinsichtlich ihres Aufwands (Fertigungszeit) und Nutzens (Pressungsverteilung) für die Praxis beispielhaft dargestellt werden. Im Folgenden wird ein Auszug der Ergebnisse vorgestellt.
Grundlagen der Korrekturauslegung
Die Auslegung der Makrogeometrie, wie zum Beispiel Achsabstand, Breite, Zähnezahl, Modul, ist vorwiegend vom Bauraum und dem zu übertragenden Drehmoment bestimmt. Sind diese Größen festgelegt, kann der Zahnkontakt detailliert analysiert werden. Basis ist die Berechnung der Belastungsverteilung auf der Zahnflanke unter Berücksichtigung der Verformungen und Abweichungen aller Komponenten des Getriebes unter Auslegungslast. Diese kann mit verschiedenen Programmen durchgeführt werden (zum Beispiel Rikor, KissSoft, Romax etc.).
Als letzter Schritt im Auslegungsprozess wird die Mikrogeometrie mittels bewusster Zahnflankenkorrekturen verändert und hinsichtlich eines definierten Zieles optimiert. Anhand von zum Beispiel Pressungsverteilung, Tragfähigkeitskennwerten und firmenspezifischen Vorgaben wird iterativ die bestmögliche Zahnflankenmodifikation ermittelt.
Eine Zahnflankenkorrektur bedeutet hierbei eine Rücknahme der Flanke um teilweise wenige Mikrometer und somit eine Entlastung des korrigierten Bereichs. Da die Summe der Gesamtlast, das zu übertragende Drehmoment, gleich bleibt, bedeutet das eine Zunahme der Last in den Flankenbereichen, die im Kontakt bleiben.
Die gewünschte Mikrogeometrie einer Verzahnung wird zumeist durch die Überlagerung mehrerer Standardkorrekturen erzielt. In DIN ISO 21771 [3] sind die Standardkorrekturarten definiert. Sie beschreiben den Flankenbereich, in dem die Korrekturen wirksam sind. Bild 1 zeigt eine Übersicht der Standardkorrekturarten.
Es werden mit den verschiedenen Korrekturarten unterschiedliche Ziele erreicht:
1. Korrekturen in Stirnprofilrichtung (Eingriffsstrecke): Allgemein werden Verzahnungsbeginn und -ende entlastet, um örtlich hohe Flankenpressungen in diesen Bereichen abzumildern. Mittels der Profilkorrekturen werden das Geräuschverhalten, der Wirkungsgrad und die Tragfähigkeit, z. B. für die Schadensform Grübchen, beeinflusst.
2. Korrekturen in Flankenlinienrichtung (Eingriffsbreite): Ungleichmäßigkeiten resultieren zumeist aus Verformungen und Verkippungen des Welle-Lager-Systems. Ziel ist eine möglichst gleichmäßige Lastverteilung über der Zahnbreite und eine Entlastung der Verzahnungsränder, um zum Beispiel bei Überlasten im Betrieb Kantenträger zu vermeiden.
3. Korrekturen in definierter Richtung (Flankenfläche): Die dreieckförmige Endrücknahme (Generated End Relief, kurz GER) verläuft in Wälzrichtung und ermöglicht eine gezielte Entlastung des Eingriffsbeginns und -endes bei Schrägverzahnungen. Die Verschränkung, welche im Vergleich zur dreieckförmigen Eckrücknahme über die gesamte Zahnflanke wirksam ist, kann als Verzahnungskorrektur verwendet werden oder als Verzahnungsabweichung, resultierend aus dem verwendeten Herstellungsprozess, in der Berechnung berücksichtigt werden.
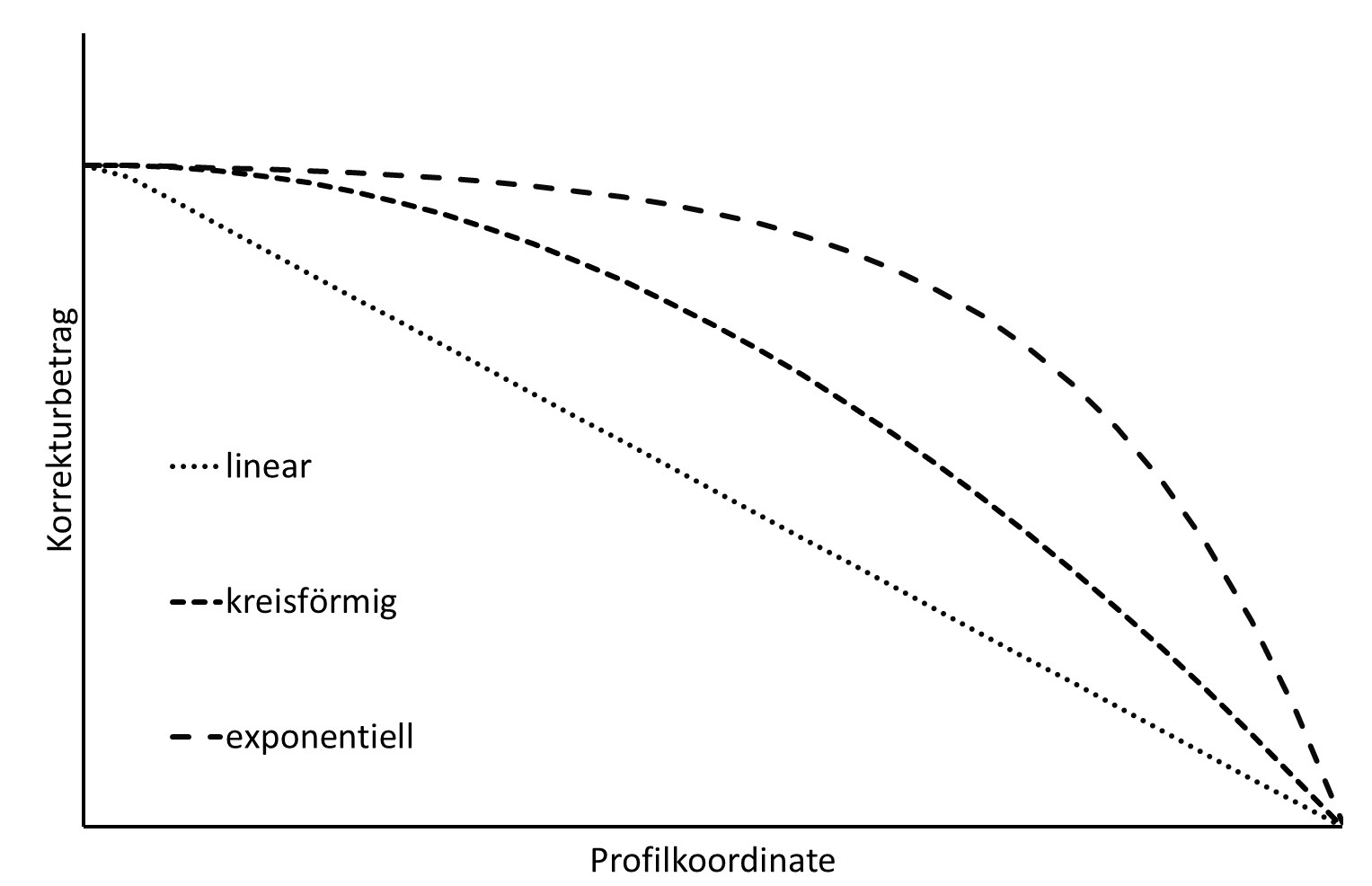
Des Weiteren ist die Form der Korrektur relevant. Sie beschreibt den Verlauf und ist z. B. in [2] beschrieben. Bild 2 zeigt die Formen linear, kreisförmig und exponentiell im Vergleich bei gleicher Korrekturlänge und gleichem Korrekturbetrag.
Die lineare Rücknahme hat den größten Materialabtrag zur Folge und somit die größte Entlastung im wirksamen Flankenbereich. Die exponentielle Rücknahme hat einen flachen Verlauf von der unkorrigierten Flanke aus und erzielt den gewünschten Korrekturbetrag mit einem steilen Verlauf am Flankenende. Dies kann für die Lastverteilung von Vorteil sein.
Entwicklungen im Wälzschleifprozess
Zur Erzeugung der Mikrogeometrie werden Stirnräder häufig geschliffen. Damit wird der Härteverzug beseitigt und eine feinere Verzahnungsqualität erzielt. Das kontinuierliche Wälzschleifen ist derzeit eines der produktivsten Verfahren und in der industriellen Praxis weit verbreitet im Einsatz. Das Werkzeug ist eine Schleifschnecke aus beispielsweise Sinterkorund. Dieses dreht sich und wird, unter anderem aus technologischen Gründen, während des Wälzvorganges entlang der Schneckenbreite verschoben. Das in Bild 3 dargestellte Verfahren kann für Gerad- und Schrägverzahnungen, für kleine und große Radabmessungen sowie für kleine Stückzahlen bis zur Serienproduktion wirtschaftlich sinnvoll eingesetzt werden.
Durch gezieltes Abrichten der Schleifschnecke sowie Steuern der Wälz- beziehungsweise Vorschubbewegung können die gewünschten Zahnflankenkorrekturen über das Profil, die Flankenlinien und entlang einer definierten Richtung aufgebracht werden.
Neben dem Schleifvorgang selbst muss auch das Abrichten der Schleifschnecke berücksichtigt werden. Dabei wird diese geschärft und geformt. Es werden so die vorgegebenen Zahnflankenkorrekturen auf die Schleifschnecke aufgebracht, welche beim Wälzschleifen in Kombination mit der Maschinenkinematik auf die Verzahnung übertragen werden. Es gibt verschiedene Arten des Abrichtens, welche Einfluss auf die umsetzbaren Korrekturen und den Zeitbedarf des Abrichtvorganges selbst haben. Lediglich die Anzahl der Werkstücke je Abrichtzyklus variiert beim diagonalen Wälzschleifen und ist im Einzelfall zu ermitteln.
Beim klassischen diagonalen Wälzschleifen von Flankenlinienkorrekturen bei Schrägverzahnungen wird die Zahnflanke verzerrt. Es wird eine ungewollte Verschränkung aufgebracht. Die gefertigte Flanke entspricht somit nicht der Sollflanke der Auslegung.
Es ist seit vielen Jahren möglich, diese natürliche Verschränkung bei Flankenlinienkorrekturen zu verhindern [12]. Neueste Entwicklungen ermöglichen dies auch verzerrungsfrei [14], wie in Bild 4 dargestellt.
Beispielauslegung
Im Folgenden werden anhand der Pressungsverteilung einer industrienahen Schrägverzahnung vier verschiedene Korrekturvarianten ausgelegt und hinsichtlich Aufwand und Nutzen diskutiert. Es werden Zahnräder aus einsatzgehärtetem 18CrNiMo-7 gewählt. Die Verzahnung wird für lange Lebensdauer mit einer Sicherheit auf der Flanke von circa 1,3 ausgelegt. Tabelle 1 zeigt die Verzahnungshauptdaten der gewählten Beispielver- zahnung.
| Modul | mn | 7,75 mm |
| Achsabstand | a | 460 mm |
| Verzahnungsbreite | b | 100 mm |
| Schrägungswinkel | ß | 13 ° |
| Übersetzung | i | 2,71 |
| Profilüberdeckung | ɛa | 1,3 |
| Sprungüberdeckung | ɛβ | 0,9 |
| Nenndrehmoment | Tnenn | 12000 Nm |
| Drehzahl am Ritzel | n | 1500 1/min |
Tabelle 1
Verzahnungshauptdaten der industrienahen Beispielschrägverzahnung
Für die Lastverteilung ist es von untergeordneter Bedeutung, wie die Korrekturen auf Ritzel und Rad aufgeteilt werden, daher werden im Folgenden alle Korrekturen für das Ritzel ausgelegt. Das Rad bleibt unkorrigiert.
Die Berechnungen sind mit dem Programm Rikor [13] erstellt worden. Rikor erlaubt die Berechnung der Lastverteilung im Zahnkontakt von Stirnradgetrieben hinsichtlich Wellenverformung, Lagerdurchsenkung, Zahnflankenkorrekturen, Lastverteilung im Zahnkontakt, schadensrelevanten Beanspruchungen und Tragbild bei gerad-, schräg- und doppelschrägverzahnten Stirnrädern [5].
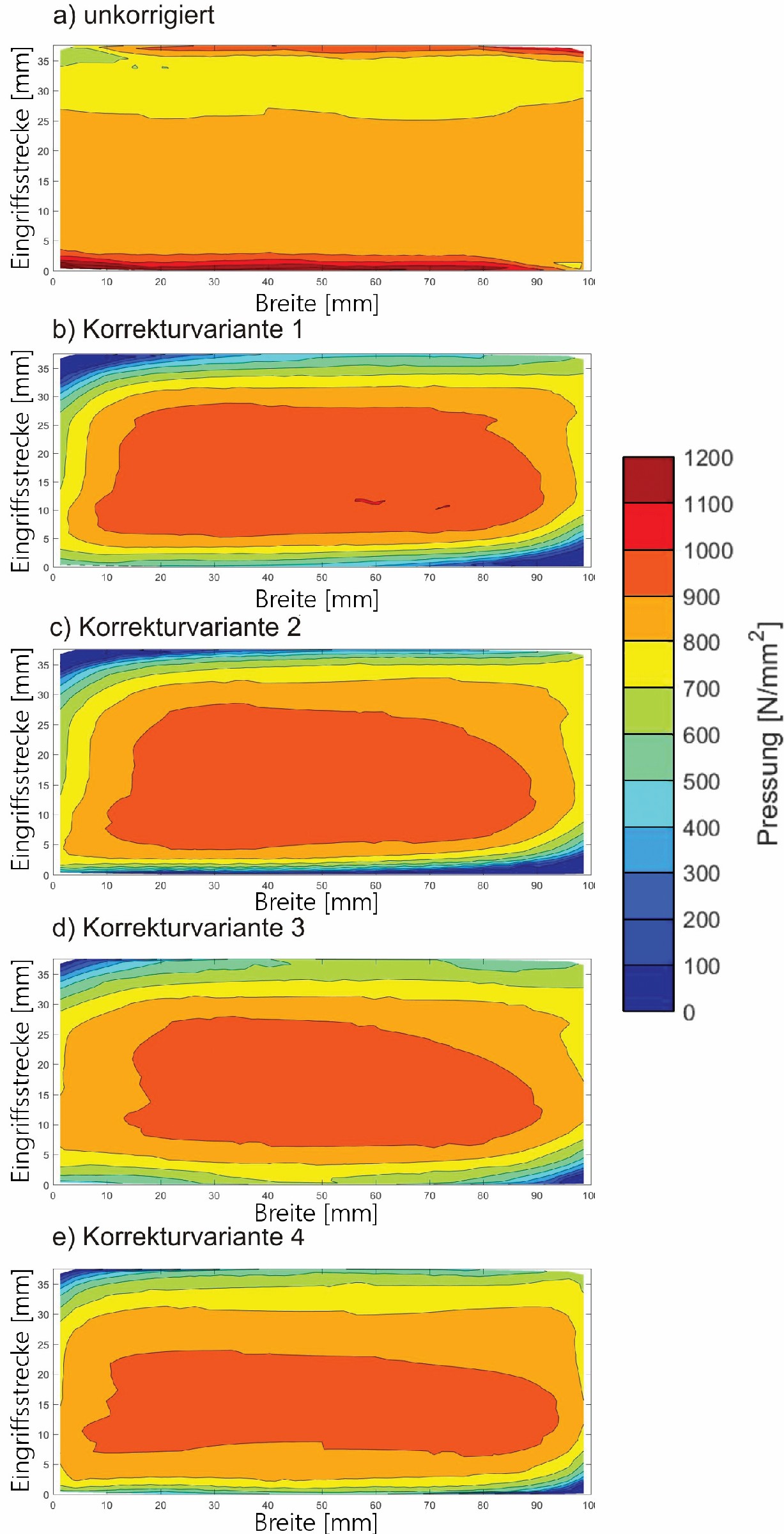
Die unkorrigierte Beispielverzahnung zeigt eine typische Pressungsverteilung mit Überhöhungen im Eingriffsbeginn und -ende sowie am Verzahnungsrand. Der Eingriffsbeginn liegt aufgrund der Richtung des Schrägungswinkels am linken Verzahnungsrand. Zudem liegt hier der kleinste Ersatzkrümmungsradius vor. Daraus resultiert bei gleicher Last eine höhere Pressung im Eingriffsende. In Bild 5a ist die Pressungsverteilung in N/mm2 über dem Eingriffsfeld für die Beispielverzahnung als flächiger Konturplot abgebildet.
Es sind deutlich die starken Pressungsüberhöhungen im Eingriffsbeginn /-ende sowie leichte Überhöhungen an den Verzahnungsrändern zu erkennen.
Um den Aspekt der Fertigung in einer Aufwandsabschätzung zu berücksichtigen, wird für alle Korrekturvarianten das Liebherr-Deviation-Free-Topological-Schleifverfahren (kurz DFT) gewählt. Es erlaubt in einer angepassten Form auch dreiecksförmige gewälzte Endrücknahmen (GER) abweichungsfrei zu fertigen. Hierbei können die gleichen Schleif- und Abrichtzeiten erreicht werden wie beim DFT-Schleifverfahren [6], [14]. Die geometrischen Randbedingungen bzw. Einschränkungen sind im Einzelfall zu überprüfen.
Korrekturvariante 1
Variante 1 ist eine Kombination aus kurzer Kopf- und Fußrücknahme nach Sigg [7], überlagert mit einer leichten Flankenlinienballigkeit und -endrücknahmen. Alle Korrekturen sind linear mit einer Übergangsrundung vom korrigierten zum unkorrigierten Bereich ausgeführt (Korrekturdaten siehe Tabelle 2).
| Korrekturart | Korrekturform | Korrekturbetrag | Korrekturlänge | Korrekturübergang |
| Profilrichtung | ||||
| Kopfrücknahme | linear | 32 µm | 7,08 mm (kurz) | Beginn 3 mm Ende 12 mm |
| Fußrücknahme | linear | 38 µm | 7,08 mm (kurz) | Beginn 3 mm Ende 12 mm |
| Flankenlinienrichtung | ||||
| Balligkeit | symmetrisch | 7 µm | – | – |
| Endrücknahme links | linear | 8 µm | 15 mm | Beginn 7,5 mm Ende 40 mm |
| Endrücknahme rechts | linear | 4 µm | 15 mm | Beginn 7,5 mm Ende 40 mm |
Tabelle 2
Korrekturangaben für Korrekturvariante 1
Aufgrund der höheren Pressungen im Eingriffsbeginn als im -ende, sind die Korrekturen über das Profil und in Flankenlinienrichtung unsymmetrisch.
Bild 5b zeigt die Pressungsverteilung. Sie ist ausgewogen und gleichmäßig.
Korrekturvariante 2
Für Variante 2 werden die Korrekturen aus Variante 1 verwendet und, außer der Balligkeit, die Korrekturformen von linear auf exponentiell ge-ändert.
Bild 5c zeigt die Pressungsverteilung. Der exponentielle Verlauf der Korrekturen schafft eine bessere Ausnutzung der Randbereiche der Zahnflanke.
Korrekturvariante 3
In Variante 3 wird das GER eingesetzt. Sie wird mit im Vergleich zu Variante 1 und 2 reduzierter Kopf- und Fußrücknahme und leicht vergrößerter Flankenlinienballigkeit kombiniert. Alle Korrekturarten, außer der Balligkeit, sind linear mit Übergangsrundung ausgeführt (Korrekturdaten siehe Tabelle 3).
| Korrekturart | Korrekturform | Korrekturbetrag | Korrekturlänge | Korrekturübergang |
| Profilrichtung | ||||
| Kopfrücknahme | linear | 23 µm | 7,08 mm (kurz) | Beginn 3 mm Ende 12 mm |
| Fußrücknahme | linear | 25 µm | 7,08 mm (kurz) | Beginn 3 mm Ende 12 mm |
| Flankenlinienrichtung | ||||
| Balligkeit | symmetrisch | 9 µm | – | – |
| Flankenfläche | ||||
| GER Kopf | linear | 10 µm | 7,08 mm (kurz) | Beginn 7 mm Ende 22 mm |
| GER Fuß | linear | 15 µm | 7,08 mm (kurz) | Beginn 7 mm Ende 22 mm |
Tabelle 3
Korrekturangaben für Korrekturvariante 3
Bild 5d zeigt die Pressungsverteilung. Sie ist vergleichbar mit Variante 2. Die gezielte Rücknahme der lastüberhöhten Eckbereiche des Eingriffbeginns und -endes ermöglichen eine Verringerung der Beträge der Kopf- und Fußrücknahme sowie einen Verzicht auf die Endrücknahme bei leicht größerer Flankenlinienballigkeit.
Korrekturvariante 4
In Variante 4 werden die Korrekturen aus Variante 3 verwendet und, außer der Balligkeit, exponentiell statt linear umgesetzt.
Bild 5e zeigt die Pressungsverteilung. Es zeigt sich erneut der Vorteil des exponentiellen Korrekturverlaufs. Es konnte im Vergleich zum linearen Verlauf (Variante 3) eine gleichmäßigere Pressungsverteilung erreicht werden.
Vergleich der Varianten
Neben dem reinen visuellen Vergleich der Pressungsverteilung über dem Eingriffsfeld bietet sich die schadensäquivalente Beanspruchung nach FVA 284 [9], [10], als Vergleichsgröße an. Sie wird zur Bestimmung der Tragfähigkeit einer Verzahnung gegen die Schadensform Grübchen verwendet und wird aus der Pressungsverteilung eines Zahnrades unterhalb des Wälzkreises ermittelt. In ihr gehen der Maximalwert und die Verteilung der Pressungen ein. Eine niedrige schadensäquivalente Beanspruchung kann als Hinweis auf eine belastungsgünstige Verteilung der Pressungen angesehen werden.
In Tabelle 4 sind die schadens- äquivalenten Beanspruchungen nach FVA 284 für die vier Korrekturvarianten aufgeführt. Zusätzlich ist die Differenz zur Korrekturvariante 1 in Prozent angegeben.
| Schadensäquivalente Pressung nach FVA 284 für das Rad
in N/mm2 |
Differenz der schadensäquivalenten Beanspruchung zur Korrekturvariante 1
in % |
|
| Korrekturvariante 1 | 1022,8 | 0 |
| Korrekturvariante 2 | 1004,9 | 1,75 |
| Korrekturvariante 3 | 982,6 | 3,93 |
| Korrekturvariante 4 | 965,9 | 5,56 |
Tabelle 4
Vergleich der Korrekturvarianten
Der Vergleich zeigt, dass sich die Verwendung von exponentiellen Korrekturen lohnt. Es kann ein Tragfähigkeitsgewinn von 1,75 % erreicht werden. Bei Anwendung von dreiecksförmigen gewälzten Endrücknahmen (GER) kann im Vergleich zur Kombination aus Kopf-, Fuß- und Endrücknahmen eine Reduzierung der Beanspruchung um knapp 4 % erreicht werden. Werden die Korrekturen zusätzlich exponentiell statt linear mit Übergangsrundung ausgeführt, kann im gezeigten Beispiel die Beanspruchung um gut 5 % reduziert werden.
Die Korrekturen von Variante 1 stellen den Stand der Technik dar und können abweichungsfrei mit dem Liebherr-DFT-Verfahren in der Serienfertigung geschliffen werden. Die Fertigung der exponentiellen Endrücknahmen in Variante 2 ist mit dem gleichen Verfahren mit gleichem Zeitaufwand wie bei Variante 1 möglich. Die gewälzten Korrekturen GER in Variante 3 können verzerrungsfrei mit gleichem Zeitaufwand wie bei Variante 1 und 2 gefertigt werden. Die Fertigungszeit der gewälzten Korrekturen mit exponentiellen Verlauf aus Variante 4 entspricht dabei jener von Variante 3.
Beide Vorteile, der der gewälzten Korrektur und des exponentiellen Verlaufs, sind mit dem GER-Schleifverfahren in der Serienfertigung nutzbar.
Zusammenfassung
Die Mikrogeometrie der Zahnflanke hat entscheidenden Einfluss auf die Tragfähigkeit der Verzahnung. In der Verzahnungsauslegung ist die Bestimmung der idealen Verzahnungskorrektur der finale Arbeitsschritt. Die rechnerischen Möglichkeiten sind aufgrund einer Vielzahl von möglichen Korrekturarten und -formen groß. Der Vorgang der Korrekturauslegung selbst ist zeitaufwendig, da iterativ die Korrekturen angepasst werden, die bestimmenden Größen neu berechnet und ausgewertet werden müssen. Zusätzlich muss die Fertigbarkeit der Korrekturen, speziell die Fertigungszeit bei Serienfertigung, berücksichtigt werden.
Anhand einer industrienahen Beispielverzahnung wird der Nutzen von unterschiedlichen Korrekturarten und -formen als Einfluss auf die Pressungsverteilung und die schadensäquivalente Beanspruchung nach FVA 284 betrachtet. Neben der klassischen linearen Korrekturform mit Übergangsrundung, zeigt der exponentielle Korrekturverlauf signifikante Vorteile in der Pressungsverteilung und ermöglicht eine Reduzierung der schadensäquivalenten Be-anspruchung. Durch die Verwendung einer gewälzten Eckrücknahme können, im Vergleich mit einer Kombination nur aus Profil- und Flankenlinienkorrekturen, die Korrekturbeträge reduziert werden. Es ergibt sich eine bessere Ausnutzung der gesamten Zahnflanke und somit eine Verrin- gerung der schadensäquivalenten Beanspruchung. Wird dies mit den Vorteilen des exponentiellen Korrekturverlaufs überlagert, kann die schadensäquivalente Beanspruchung weiter reduziert werden.
Bei den untersuchten Korrekturvarianten wurde das Diagonalwälzschleifen vorausgesetzt, um die natürlichen Verschränkungen bei Flankenlinienkorrekturen zu eliminieren. Durch die Anwendung der Schleifverfahren Liebherr-DFT beziehungsweise -GER werden gleiche Schleif- und Abrichtzeit bei den gezeigten Korrekturvarianten erreicht. Damit erscheint eine wirtschaftliche Fertigung dieser Korrekturen gegeben und somit können die Vorteile der exponentiellen Korrekturform und der Eckrücknahme auch für die Serienfertigung genutzt werden.
Literatur
[1] Brecher, C.; Löpenhaus, C.; Theling, J.; Schroers, M.; Piel, D.: FE-Based method for design of robust tooth flank modifications for cylindrical and planetary gear stages regarding manufacturing tolerances. American Gear Manufacturers Association Fall Technical Meeting Papers 2017. Columbus, Ohio, USA, S. 148–163 (2017)
[2] Carl, C.; Stiller, S.: FVA-Nr. 609/I – Heft 1079 – Korrektureinfluss Lastverteilung, Programmanleitung zum Korrekturprogramm SEKOR. Forschungsvereinigung Antriebstechnik e.V., Frankfurt/Main (2013)
[3] DIN ISO 21771:2014–08 Zahnräder – Zylinderräder und Zylinderradpaare mit Evolventenverzahnung – Bestimmungsgrößen und Geometrie.
[4] Fuentes-Aznar, A.; Eisele, S.; Gonzalez-Perez, I.: Computerized simulation of manufacturing errors in cylindrical spur gears and their compensation through flank modifications. Mechanisms and Machine Science 51, S. 1–25 (2018)
[5] Höhn, B.-R.; Otto, M.; Thoma, F.: Calculation of load distribution and load carrying capacity for spur and helical gears. International Conference on Gears, VDI-Berichte 2108.2, München, S. 855–866 (2010)
[6] Mehr, A.; Yoders, S.: Efficient hard finishing of asymmetric tooth profiles and topological modifications by generating grinding. American Gear Manufacturers Association Fall Technical Meeting Papers 2016, Pittsburgh, Pennsylvania, USA (2016)
[7] Kohn, B.; Utakapan, T.; Fromberger, M.; Otto, M.; Stahl, K.: Flank modifications for optimal excitation behavior. Forschung im Ingenieurwesen/Engineering Research, Volume 81, Issue 2–3, 1 September 2017, S. 65–71 (2017)
[8] Sigg, H.: Profile and Longitudinal Corrections on Involute Gears. American Gear Manufacturers Association Semi-Annual Meeting, Chicago, Illinois, USA (1965)
[9] Stahl, K.: Grübchentragfähigkeit einsatzgehärteter Gerad- und Schrägverzahnungen unter besonderer Berücksichtigung der Pressungsverteilung. Dissertationsschrift. Technische Universität München, München (2001)
[10] Stahl, K.: FVA-Nr. 284/I+II – Heft 608 – Experimentelle und theoretische Untersuchungen an Schrägstirnrädern. Forschungsvereinigung Antriebstechnik e.V., Frankfurt/Main (2001)
[11] Stahl, K.; Otto, M.; Zimmer, M.: Striving for high load capacity and low noise excitation in gear design. American Gear Manufacturers Association Fall Technical Meeting 2013, Indianapolis, Indiana, USA, S. 138–151 (2013)
[12] Sulzer, G.: Patentnummer DE 3704607 A1. München: Deutsches Patentamt (1988)
[13] Weinberger, U.: Benutzeranleitung Rikor. Forschungsvereinigung Antriebstechnik e.V., Frankfurt/Main (2017)
[14] Wuerfel, R.; Geiser, H.: New macro and micro geometries of generated ground gears. International Conference on Gears Production 2015, VDI-Bericht 2255, München, S. 1419–1428 (2015)
Sabrina Bansemir, M. Sc.
Dr.-Ing. Michael Otto Prof.
Dr.-Ing. Karsten Stahl
alle: Lehrstuhl für Maschinenelemente Forschungsstelle für Zahnräder und Getriebe- bau (ZFG),
TU München, Boltzmannstr. 15n 85748 Garching
Tel.: 0 89 / 2 89-1 58 07 E-Mail: fzg@fzg.mw.tum.de www.fzg.mw.tum.de
Dr.-Ing. Hansjörg Geiser
Dipl.-Phys. Robert Würfel
beide: Liebherr Verzahntechnik GmbH, Kaufbeurer Straße 141, 87437 Kempten/Allgäu
Tel.: 08 31 / 7 86-0 E-Mail: info.lvt@liebherr.com www.liebherr.com


![Bild 4 Schleifergebnisse unter Verwendung verschiedener Verfahren am Beispiel einer beidseitigen Endrücknahme; gelb die Vorgabe, blau das Schleifergebnis; a) mit natürlicher Verschränkung, b) verschränkungsarm nach [12], c) verzerrungsfrei nach [14]. Bild: Verfasser](https://www.ingenieur.de/wp-content/uploads/2020/01/KA-814-Bansemir-Geiser_Bild_04.jpg)