Berücksichtigung von Wechselwirkungen zwischen Abweichungen in der statistischen Toleranzanalyse

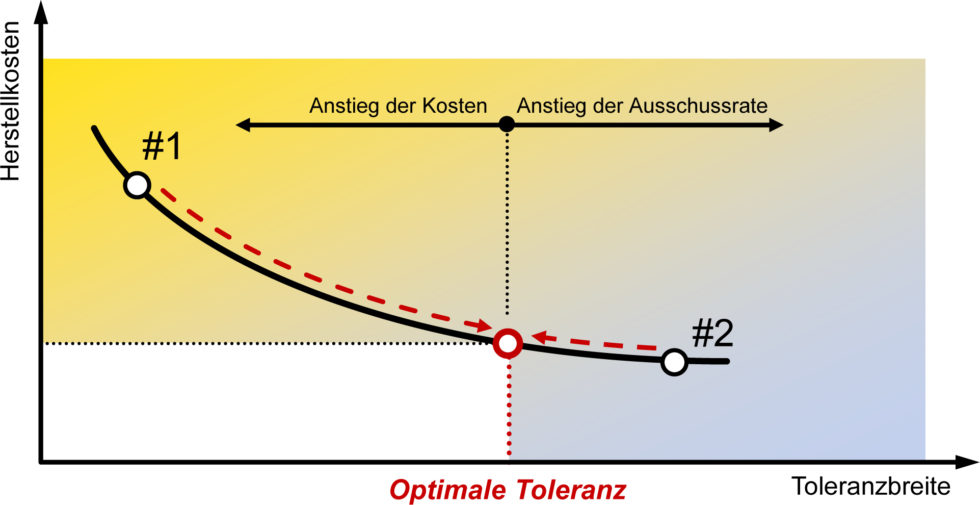
Bild 1 Konsequenzen einer unzureichenden Toleranzvergabe. Bild: Verfasser

1 Beitragsleister in der Toleranzanalyse

Statistische Toleranzanalysen werden in der Produktentwicklung eingesetzt, um die Auswirkungen von Maß-, Form- und Lageabweichungen auf funktionsrelevante Eigenschaften eines Produktes (sogenannte Schließmaße) zu evaluieren [1]. Neben der resultierenden Häufigkeitsverteilung des Schließmaßes werden insbesondere die Beitragsleister der Abweichungen bestimmt. Diese quantifizieren die Auswirkungen einer jeden Abweichung auf die resultierende Streuung des Schließmaßes. Ein hoher Beitragsleister steht hierbei für einen großen Einfluss der jeweiligen Abweichung. Hieraus folgt, dass sich bereits mit einer geringen Ein- engung der Toleranz eine signifikante Reduzierung der Schließmaßstreuung erreichen lässt. Hingegen impliziert ein geringer Beitragsleister eine geringe Sensitivität des Schließmaßes gegenüber dieser Toleranz. Somit besteht die Möglichkeit, durch gezielte Aufweitung dieser Toleranz die Herstellkosten des Produktes zu senken.

Im Rahmen der statistischen Toleranzrechnung werden gegenwärtig Methoden der lokalen Sensitivitätsanalyse zur Berechnung der Beitragsleister angewendet. Hervorzuheben sind hierbei die High-Low-Median-Analyse (kurz: HLM-Analyse) [2] sowie die analytische Bestimmung der statistischen Beitragsleister nach [3].

Jedoch berücksichtigen diese lokalen Methoden lediglich direkte Auswirkungen der Abweichungen auf das Schließmaß. Mögliche Wechselwirkungen zwischen den Abweichungen (und die damit verbundenen zusätz- lichen indirekten Auswirkungen auf das Schließmaß) werden bisher nicht berücksichtigt. Die Vergabe von Toleranzen durch den Produktentwickler basiert somit oftmals auf unzureichenden Analyseergebnissen und ist somit in keinem Fall optimal. Die Konsequenzen sind mitunter erheblich, da hierdurch Fehleinschätzungen der tatsächlichen Toleranzsituation unvermeidbar sind. So kann sich eine vermeintlich optimierte Toleranzspezifikation als zu konservativ (zu enge Toleranzen) und damit als zu teuer oder als zu wohlwollend (steigende Ausschussraten aufgrund zu weiter Toleranzen) entpuppen. Die beiden Szenarien #1 und #2 in Bild 1 verdeutlichen dies.

2 Globale varianzbasierte Sensitivitätsanalyse

Die Sensitivitätsanalyse dient zur Untersuchung, „in wie weit die Variation eines Ausgangsparameters auf die Variation von Eingangsparametern zurückgeführt werden kann“ [5]. Der Zusammenhang zwischen dem funktionsrelevanten Schließmaß SM und den abweichungsbehafteten Einzel-maßen M_i wird durch eine Funktion f beschrieben. Die Einzelmaße M_i unterliegen hierbei Abweichungen, welche jeweils innerhalb ihrer Toleranz nach zugehörigen Häufigkeitsverteilungen (z. B. Normalverteilung) verteilt sind.

SM = f (M₁, M₂, …, M_i)

Die globale Sensitivitätsanalyse basiert auf der Zerlegung der Schließmaßvarianz Var[SM] in zwei Terme.

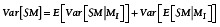
Hierbei entspricht E[SM|M_I] dem bedingten Erwartungswert und Var [SM|M_I] der bedingten Varianz von SM, bezogen auf M_I. M_I ist ein Vektor, der sich aus Zufallswerten der Einzelmaße M_i zusammensetzt. Der bedingte Erwartungswert E[SM|M_I] ist der erwartete Wert des Schließmaßes für den Fall, dass die Einzelteilabweichungen bereits bekannt sind. Analoges gilt für die bedingte Varianz. Somit lassen sich Haupteffekt S_i und Totaleffekt S_Ti jeder Einzelteiltoleranz bestimmen. M_~i bezeichnet alle Toleranzen außer der betrachten i-ten Toleranz.

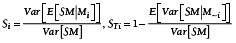
Der Haupteffekt quantifiziert die direkten Auswirkungen eines abweichungsbehafteten Einzelmaßes M_i auf das Schließmaß. Hingegen beschreibt der Nebeneffekt die indirekten Auswirkungen dieser Abweichung auf das Schließmaß aufgrund von Wechselwirkungen mit anderen Abweichungen. Die Summe aus Haupt- und Nebeneffekt des Einzelmaßes M_i wird als Totaleffekt S_Ti bezeichnet. Somit gilt stets:

S_i ≤ S_Ti

Zur Bestimmung der Varianzen lassen sich zwei Gruppen stichprobenbasierter Ansätze unterscheiden [5]: Zufallszahlenbasierte Methoden (Sobol Indizes) und spektrale Methoden (Extended Fourier Amplitude Sensitivity Test; kurz: EFAST). Bei erstgenannter Methode wird die Funktion f in Terme mit steigender Dimension überführt. Diese Terme sind paarweise orthogonal und ermöglichen die Bestimmung der Varianzen durch geeignete Integrationsverfahren. Bei EFAST wird der Erwartungswert des Schließmaßes durch eine Fourier-Reihe angenähert. Mittels der Fourier-Koeffizienten können anschließend die Varianzen approximiert werden. Für weitere Ausführungen sei auf [5] verwiesen.

3 Statistische Toleranzanalyse eines Scharniers

Bild 2 Scharnier zum Öffnen einer Abdeckung. Bild: Verfasser

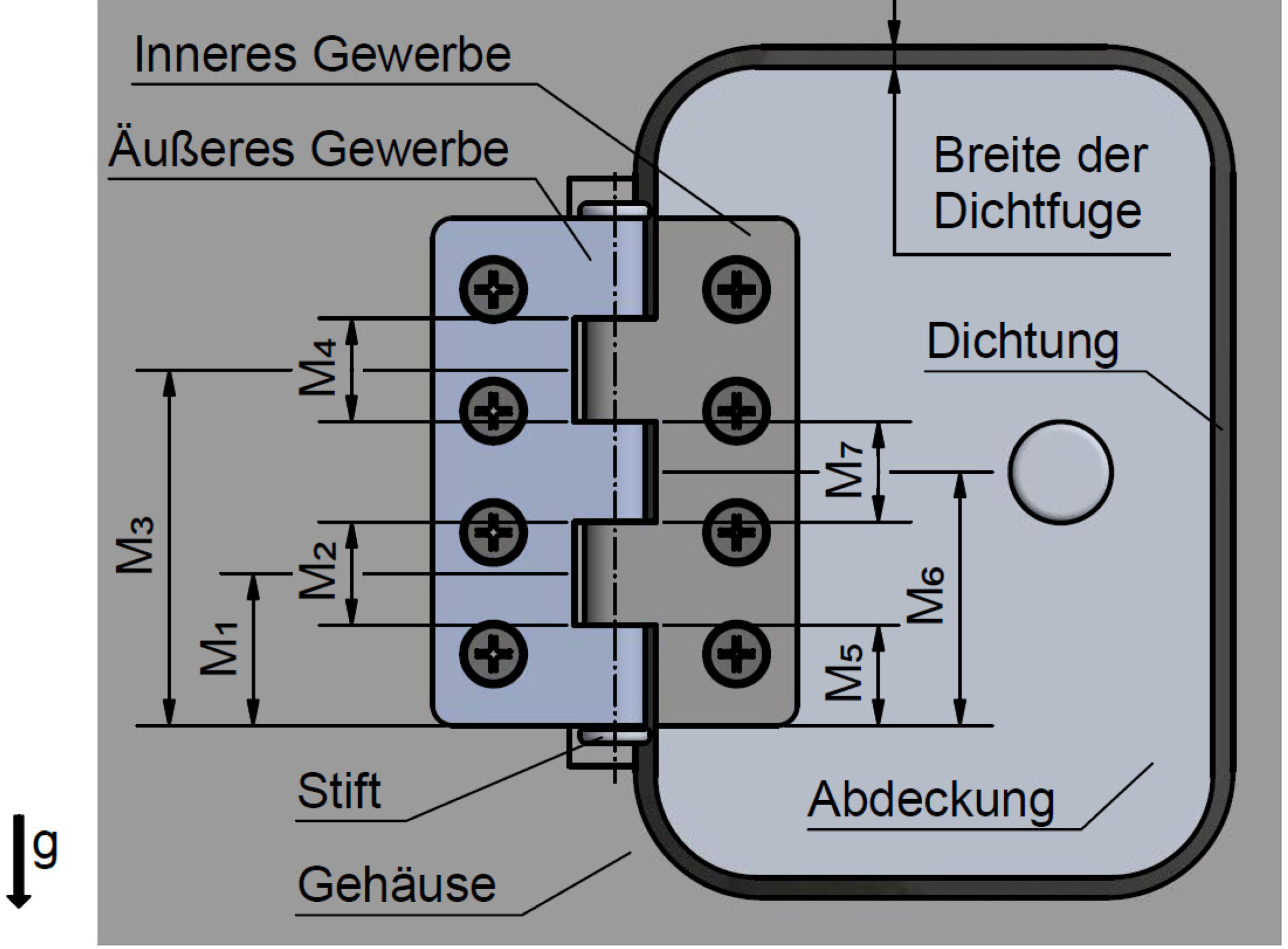
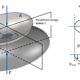
Die Auswirkungen von Wechselwirkungen zwischen Abweichungen werden am Beispiel eines abweichungs- behafteten Scharniers (Bild 2, in Anlehnung an [6]) aufgezeigt.

Hierbei sei bereits vorausgenommen, dass diese vermeintlich „einfache“ Baugruppe (die Annahme einer eindimensionalen Schließmaßgleichung mit rein linearen Abhängigkeiten liegt nahe), jedoch signifikant durch Wechselwirkungen zwischen den auftretenden Abweichungen beeinflusst wird.

Das Scharnier besteht aus zwei flächigen Bauteilen (den Gewerben), die mit einem Stift verbunden sind. Das Scharnier ermöglicht das Öffnen und Schließen einer Abdeckung. Aufgrund fertigungsbedingter Abweichungen der Maße M₁ bis M₇ resultiert eine Streuung der vertikalen Position der Abdeckung. Um jedoch eine ausreichende Dichtwirkung der Abdeckung sicherzustellen, soll die vertikale Abweichung der Abdeckung bei mindestens 99,73 % (entspricht einer 6s-Forderung) aller hergestellten Scharniere innerhalb einer zulässigen Streuung von 0,210 mm liegen. Mittels einer statistischen Toleranzanalyse wird im Folgenden untersucht, ob die bestehende Tolerierung (Tabelle 1) diese Anforderung erfüllt sowie gegebenenfalls notwendige Änderungen an der Tolerierung abgeleitet.

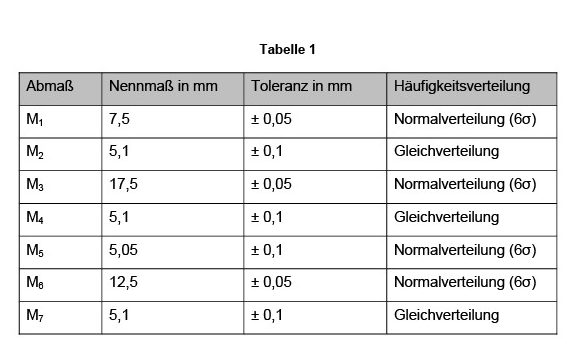
Tabelle 1 Abmessungen und zugehörige Toleranzen des Scharniers.

Die bestehende Tolerierung umfasst hierbei Toleranzen, die den in Toleranzanalysen meist betrachteten Häufigkeitsverteilungen der Normalverteilung und der Gleichverteilung folgen. Das betrachtete Schließmaß der Baugruppe ist die vertikale Verschiebung des inneren Gewerbes gegenüber dem äußeren Gewerbe des Scharniers, die unmittelbar die Breite der Dichtfuge der Abdeckung beeinflusst.

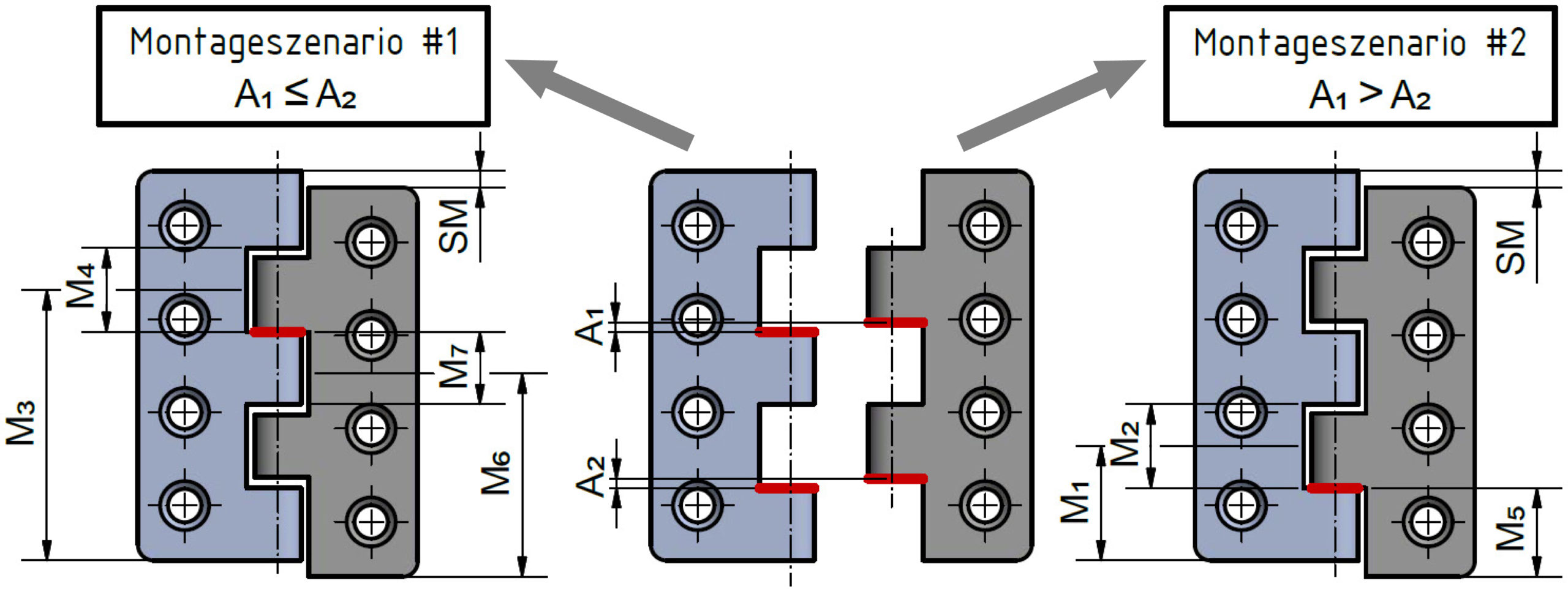
Für die statistische Toleranzanalyse muss zunächst der mathematische Zusammenhang zwischen dem Schließmaß SM und den abweichungsbehafteten Abmessungen M₁ bis M₇ formuliert werden – die sogenannte Schließmaßgleichung. Bereits hierbei kommt die Besonderheit der Baugruppe zum Tragen: Aufgrund der konstruktiven Gestaltung des Scharniers und des Zusammenspiels der Abweichungen sind zwei Montageszenarien möglich (siehe Bild 3).

Bild 3 Zwei Montageszenarien des Scharniers. Bild: Verfasser

Beide Montageszenarien unterscheiden sich hierbei im Kontakt der beiden Gewerbe. Während sich bei Szenario #1 die Gewerbe in der oberen Nut berühren, besteht bei Szenario #2 ein Kontakt der beiden Gewerbe in der unteren Nut (Bild 3). Somit können die Abstände A₁ (obere Nut) und A₂ (untere Nut) aus den abweichungsbehafteten Abmessungen M₁ bis M₇ bestimmt werden (Bild 3). Es folgen somit:

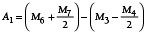
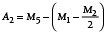
Liegt beispielsweise für ein Scharnier der Fall „A₁ ≤ A₂“ vor, so wird die Montage des Scharniers entsprechend des Montageszenarios #2 erfolgen. Das resultierende Schließmaß SM ist in diesem Fall der ermittelte Wert des Abstandes A₁. Somit resultiert eine Schließmaßgleichung in Form einer abschnittsweise definierten Funktion:

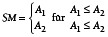
Im nächsten Schritt wird eine hohe Anzahl an Scharnieren virtuell erzeugt und montiert, sowie das resultierende Schließmaß für jede erzeugte Baugruppe mittels der Schließmaßgleichung berechnet. Im Rahmen der Untersuchungen wurde dies für 10 000 virtuelle Scharnier-Baugruppen mit einer Monte-Carlo-Simulation durchgeführt.

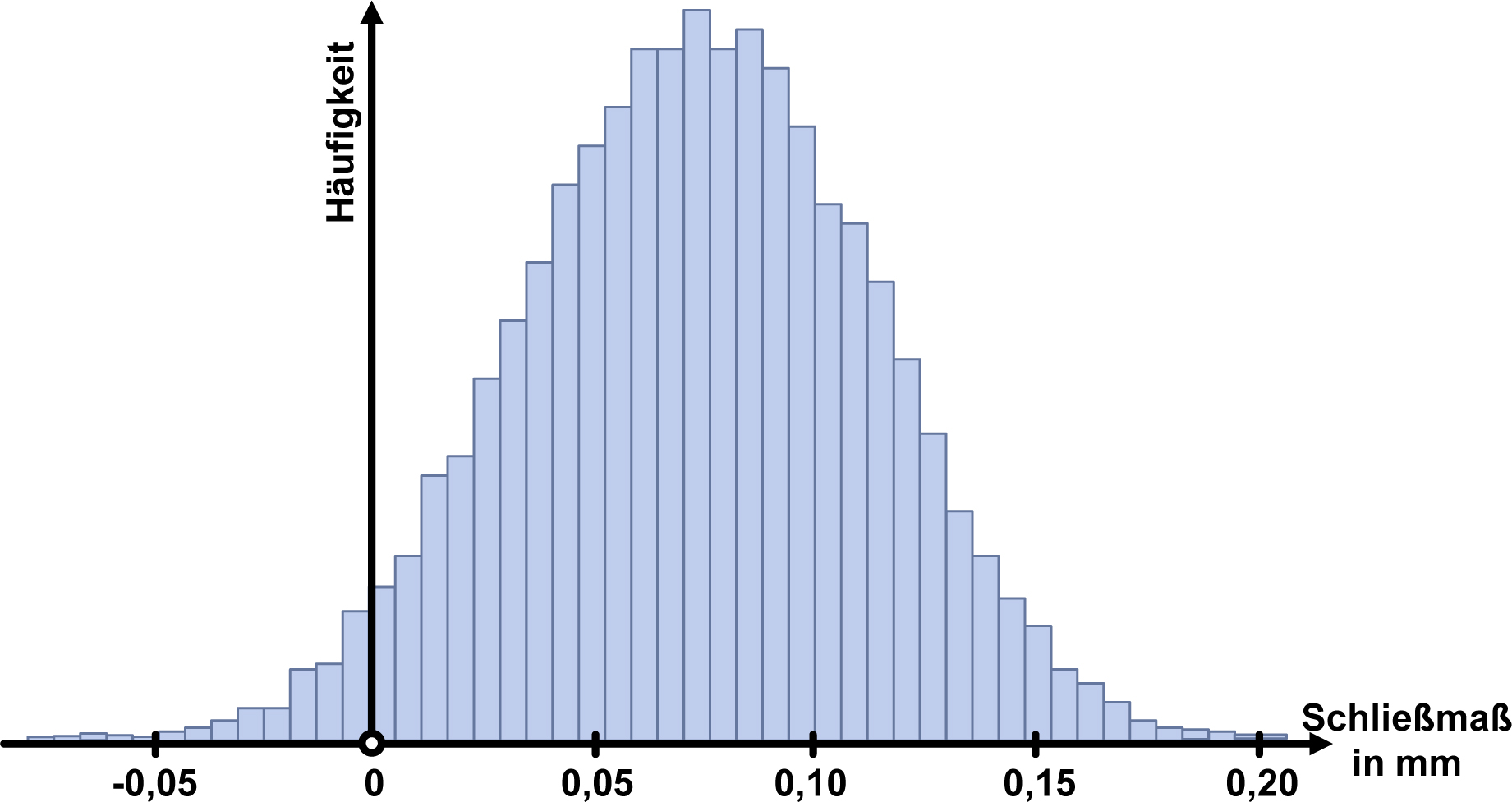
Die Darstellung des Schließmaßes erfolgt hierbei üblicherweise in Form eines Histogramms (Bild 4).

Bild 4 Resultierende Häufigkeitsverteilung des Schließmaßes. Bild: Verfasser

Die bisherige Tolerierung der Scharnierbauteile führt zu einer Schließmaßstreuung von 0,235 mm (6s). Somit wird die zulässige Streuung des Schließmaßes von 0,210 mm nicht eingehalten. Der Produktentwickler steht somit vor der Aufgabe, die Toleranzen gezielt zu ändern, um die Einhaltung der gegebenen Grenzen des Schließmaßes sicherzustellen. Als Grundlage hierfür dienen die Ergebnisse der Beitragsleister-Analyse. Die Berechnung der statistischen Beitragsleister nach [3] kann jedoch für das vorliegende Problem nicht angewendet werden, da hierfür die sogenannten Linearitätskoeffizienten a_i (partielle Ableitungen der Schließmaßgleichung) erforderlich sind. Deren Bestimmung ist jedoch im vorliegenden Fall einer abschnittsweise definierten Schließmaßgleichung nicht mehr eindeutig möglich. Hingegen sind die lokale HLM-Analyse sowie die globale Sensitivitätsanalyse (nach EFAST) auch auf derartige nicht-lineare Probleme anwendbar. Bild 5 zeigt die Ergebnisse der beiden Analysen.

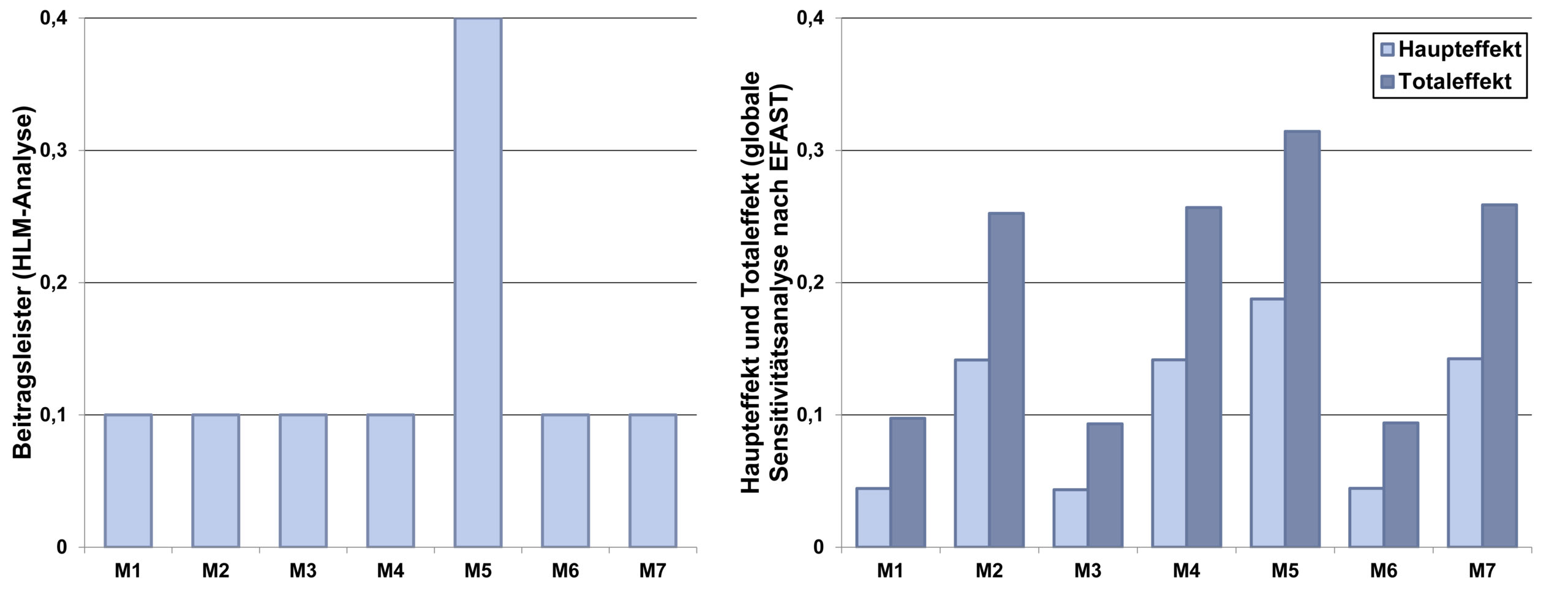
Bild 5 Ergebnisse der Beitragsleister-Analysen mittels der HLM-Analyse (links) und der globalen Sensitivitätsanalyse nach EFAST (rechts). Bild: Verfasser

Es zeigen sich grundsätzliche Ähnlichkeiten, jedoch auch drei signifikante Unterschiede in den Ergebnissen der Beitragsleister-Analysen und somit auch in den ergriffenen Maßnahmen bei der Anpassung der Toleranzen. Diese Unterschiede werden im Folgenden kurz näher erläutert:

1. Die Toleranz von M₅ ist bei beiden Analysen der größte Beitragsleister. Jedoch wird dieser Beitrag bei der HLM-Analyse weitaus größer beurteilt als bei der globalen Analyse. Dies ist darauf zurückzuführen, dass in einer HLM-Analyse nur die oberen und unteren Grenzmaße der Toleranzen berücksichtigt werden. Die jeweiligen Häufigkeitsverteilungen der Toleranzen gehen (im Unterschied zur globalen Berechnung) nicht in die Berechnung ein. Die HLM-Analyse kann somit als eine „worst-case-Beitragsleisterberechnung“ verstanden werden. Im vorliegenden Fall wird somit der Beitrag der normalverteilten Toleranz von M₅ überbewertet.
2. Die Beiträge der verbleibenden Toleranzen werden bei der HLM-Analyse als gleich groß beurteilt, während bei der globalen Analyse die Beiträge von M₁, M₃ und M₆ (alle normalverteilt) wesentlich geringer als die Beiträge von M₂, M₄ und M₇ (alle gleichverteilt) sind. Dies beruht ebenfalls auf der fehlenden Berücksichtigung der Verteilungsformen im Rahmen der HLM-Analyse.
3. Die globale Analyse zeigt, dass alle Toleranzen sowohl direkte (Haupt-effekt) als auch indirekte Effekte (Nebeneffekt = Differenz zwischen Total- und Haupteffekt > 0) zeigen. Somit bestehen Wechselwirkungen zwischen den einzelnen Abweichungen, die signifikante Auswirkungen auf das Schließmaß haben. Im betrachteten Beispiel beruhen die Wechselwirkungen darauf, dass die Fallunterscheidung in der Schließmaßgleichung durch das Zusammenspiel aller Abweichungen bestimmt wird. Diese Wechselwirkungen können mit der HLM-Analyse nicht identifiziert werden.

Der Produktentwickler ist somit in der Lage, die Toleranzen auf Basis der Beitragsleister-Analysen gezielt anzupassen. Die ergriffenen Maßnahmen unterscheiden sich jedoch aufgrund der jeweils zugrunde liegenden Analyse:

• Toleranzanpassung auf Basis der HLM-Analyse: Um die gewünschte Reduzierung der Schließmaßstreuung zu erreichen, empfiehlt sich laut der HLM-Analyse eine starke Einengung der Toleranz von M₅. Von einer Einengung der verbleibenden Toleranzen ist jedoch aufgrund ihrer geringen Beitragsleister abzusehen.
• Toleranzanpassung auf Basis der globalen Sensitivitätsanalyse: Aus den Ergebnissen der globalen Analyse folgt, dass die erforderliche Toler- anzeinengung auf die vier größten Beitragsleister (M₂, M₄, M₅ und M₇) verteilt werden kann. Die Einengung dieser Toleranzen kann zudem geringer ausfallen, da aufgrund der bestehenden Wechselwirkungen zwischen den Abweichungen, die Einengung einer Toleranz auch die indirekten Effekte weiterer Toleranzen reduziert.

Die angepassten Toleranzen beider Analysen sind in Tabelle 2 gezeigt. Es ist deutlich erkennbar, dass die Ein- engung von M₅ (HLM-Analyse) größer (±0,1 –> ±0,05) als die der Toleranzen von M₂, M₄, M₅ und M₇ (±0,1 –> ±0,08; globale Analyse) ausfallen muss, um die Anforderung an die Schließmaßstreuung zu erfüllen. Eine Aufweitung von Toleranzen ist somit im Fall der HLM-Analyse wirtschaftlich nicht möglich. Die Toleranzen M₁, M₃ und M₆ haben aufgrund ihrer äußerst geringen Beitragsleister (globale Analyse) kaum Einfluss auf das Schließmaß. Somit können durch deren gezielte Aufweitung die Fertigungskosten reduziert werden.

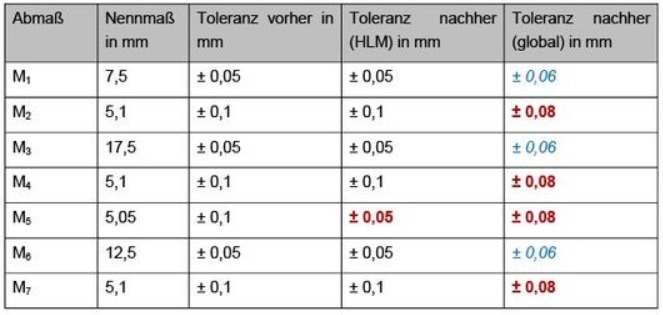
Tabelle 2 Anpassung der Toleranzen auf Basis der HLM-Analyse und der globalen Sensitivitätsanalyse nach EFAST (rot = Einengung der Toleranz; blau = Aufweitung der Toleranz)

Unter der Annahme eines quadratisch reziproken Zusammenhangs zwischen der Toleranzbreite und den zugehörigen Herstellkosten (Halbierung der Toleranzbreite führt zu Vervierfachung der Kosten), steigen somit die Herstellkosten im Fall „HLM“ auf ~119 % der Ausgangskosten. Hingegen können durch die Toleranzanpassung auf Basis der globalen Analyse die Herstellkosten sogar um rund 9 % gesenkt werden.

4 Zusammenfassung und Ausblick

Der Produktentwickler steht täglich vor der Aufgabe, Toleranzen so „eng wie nötig und so weit wie möglich“ zu vergeben. Vor diesem Hintergrund ist eine ganzheitliche Betrachtung der Auswirkungen aller Abweichungen eines Produktes essentiell, um eine optimale Toleranzvergabe und damit eine wirtschaftliche Herstellung sicherzustellen [7]. Die Grundlage aller Anpassungen an Toleranzen sind die Ergebnisse einer Beitragsleister-Analyse. Diese Analyse ist jedoch mit gängigen lokalen Methoden (z. B. HLM-Analyse) nicht in der Lage, das mitunter hochkomplexe Zusammenspiel der Abweichungen vollständig zu beschreiben. In diesem Beitrag wurden die Vorteile des Einsatzes der globalen Sensitivitätsanalyse zur Bestimmung der Beitragsleister aufgezeigt. Hierdurch ist es möglich, neben den direkten Auswirkungen der Abweichungen auf das Schließmaß auch indirekte Effekte der Abweichungen, über die Wechselwirkung mit weiteren Abweichungen, zu quantifizieren. Am Beispiel eines abweichungsbehafteten Scharniers konnten die Auswirkungen der Wechselwirkungen von Abweichungen aufgezeigt und anschließend gezielt eingeschränkt werden.

Demnach appellieren die Autoren an die Entwickler verfügbarer Toleranz-analyse-Tools, die gegenwärtig umgesetzten lokalen Ansätze zur Berechnung der Beitragsleister zu hinterfragen und die Implementierung globaler Sensitivitätsanalysen voranzutreiben. Darüber hinaus sei dem Produktentwickler, welcher unmittelbar aus den Ergebnissen der Beitragsleister-Analyse Modifikationen der Tolerierung ableiten muss, ein kritischer Umgang mit den statistischen Beitragsleistern ans Herz gelegt. Nur weil bei der bisherigen lokalen Beitragsleister-Analyse keine Wechselwirkungen zwischen Abweichungen erfasst werden, können diese dennoch vorliegen und mitunter signifikanten Einfluss auf das Schließmaß haben.

Danksagung: Die Autoren danken der Deutschen Forschungsgemeinschaft für die Förderung des Forschungsvorhabens WA2913/8-3 sowie den drei Gutachtern für Zuspruch und konstruktive Kritik.

Literatur

[1] Wartzack, S.; Meerkamm, H.; Stockinger, A.; Stoll, T.; et al.: Lebenszyklusorientierte Toleranzsimulation zur funktionalen und ästhetischen Produkt- absicherung. Konstruktion Bd. 63 (2011) Nr. 6, S. 63–67.

[2] Lin, C.-Y.; Huang, W.-H.; Jeng, M.-C.; Doong, J.-L.: Study of an assembly tolerance allocation model based on Monte Carlo simulation. Journal of Materials Processing Technology Bd. 70 (1997) Nr. 1–3, S. 9–16.

[3] Mannewitz, F.: Baugruppenfunktions- und prozessorientierte Toleranzaufweitung (Teil 1). Konstruktion Bd. 57 (2005) Nr. 10, S. 87–93.

[4] W alter, M.; Sprügel, T.; Wartzack, S.: Tolerance analysis of systems in motion taking into account interactions between deviations. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture Bd. 227 (2013) No. 5, S. 709–719.

[5] Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; et al.: Global Sensitivity Analysis – The Primer. 1. Aufl., Chichester, UK: John Wiley & Sons, 2008.

[6] Altschul, R. E.; Scholz, F. W.: Case Study in Statistical Tolerancing. Manufacturing Review Bd. 7 (1994) Nr. 1, S. 52–56.

[7] Walter, M.; Storch, M.; Wartzack, S.: On uncertainties in simulations in engineering design: A statistical tolerance analysis application. Simulation Bd. 90 (2014) No. 5, S. 547–559.