Lebensdaueruntersuchung von Gasturbinengehäusen unter Berücksichtigung geometrischer Streuungen
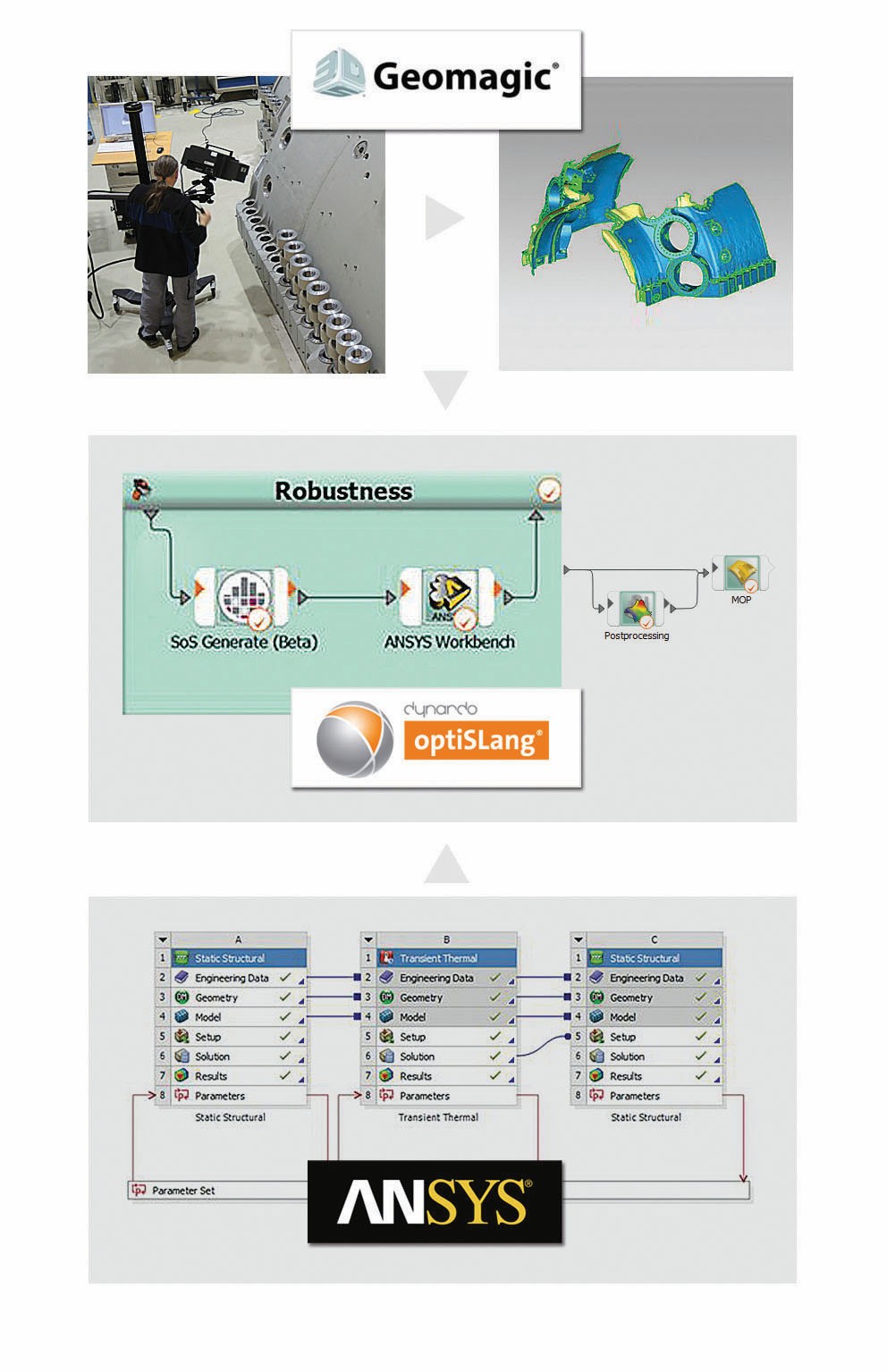
Die Siemens AG produziert große Gasturbinen zur Stromerzeugung, wie z. B. die SGT5–8000H mit 400 MW oder die CCPP bis 600 MW. Für die probabilistische Analyse geometrischer Variationen und deren Einfluss auf die Lebensdauer der Gasturbinengehäuse setzt das Unternehmen verschiedene Softwarelösungen ein, u. a. „Ansys“, „Statistics on Structures“ (SoS) und „optiSLang“. Der Beitrag schildert die Vorgehensweise der Entwickler.
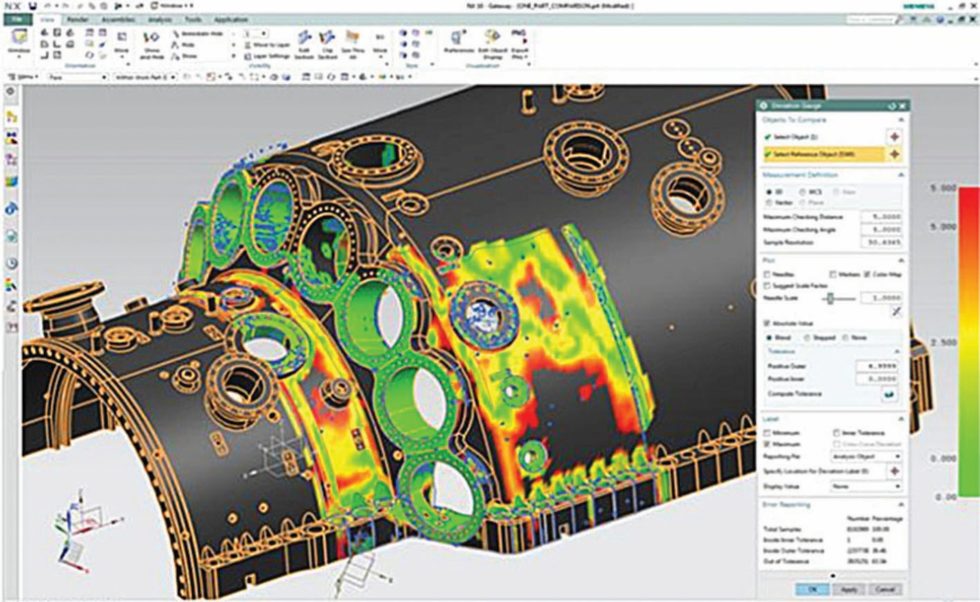
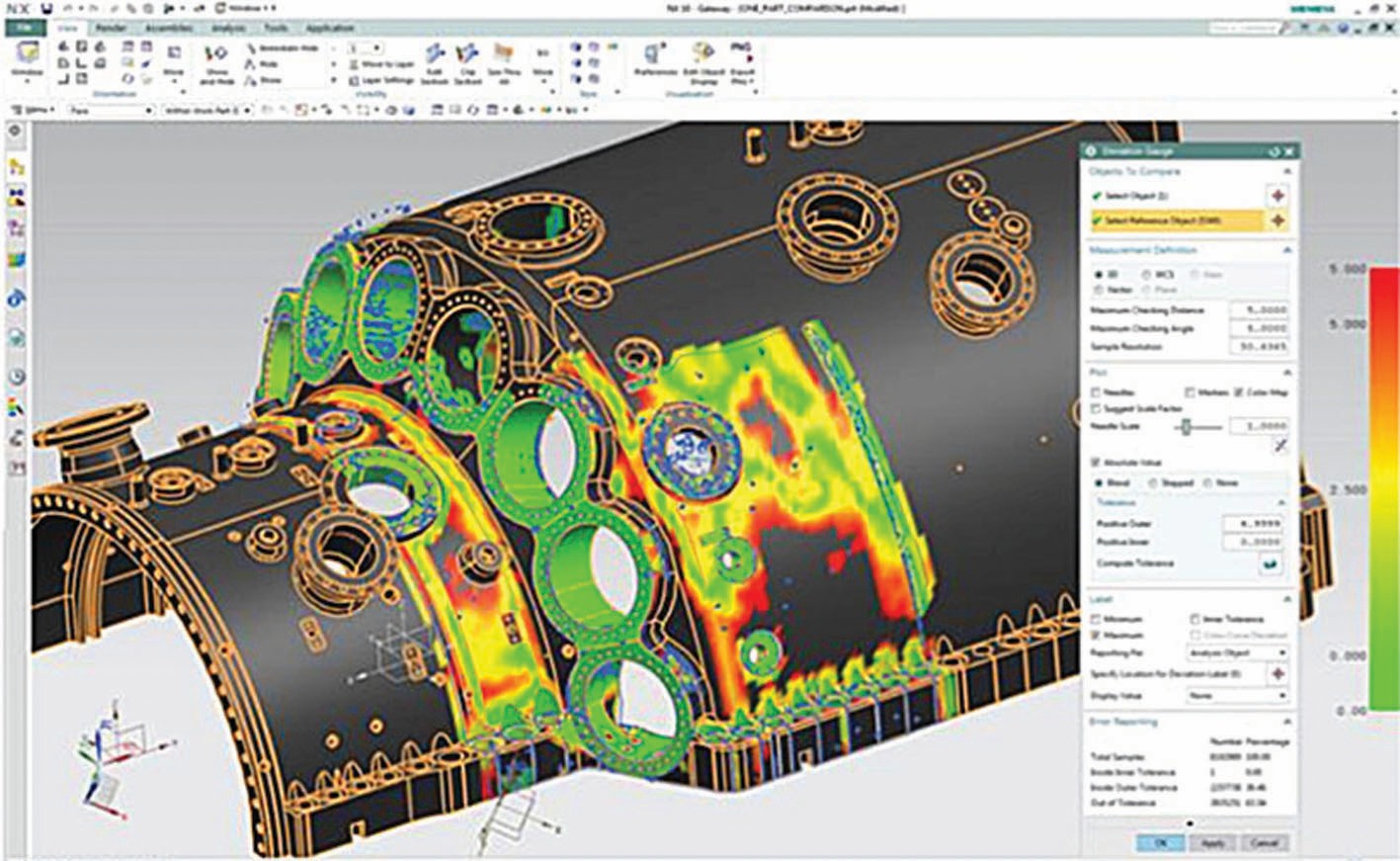
Nachbearbeitung der Laserscan-Daten in Siemens NX. Bild: Siemens
1 Motivation
Die Gasturbinen (GT) der Siemens AG (Large Gas Turbines) sind bekannt für ihre hohe Effizienz (GT mit 40 % und Gas-und-Dampfturbinen mit mehr als 60 %). Kunden erwarten Stromerzeugungsanlagen, die effizient, zuverlässig, verfügbar, flexibel und kostengünstig sind. Der gestiegene Wettbewerb im Bereich der erneuerbaren Energien verlangt von den Kraftwerksbetreibern eine ständige Verbesserung der Wirtschaftlichkeit ihrer Anlagen. Das führt zu Überlegungen, ob man Sicherheitsfaktoren und Lebensdauer neu definieren, Wartungs- und Prüfintervalle erhöhen oder einfach neue technische Lösungen finden kann. In jedem Fall erfordert eine Optimierung von Konstruktionen und Wartungszyklen auch eine Grenzwertanalyse der Produktleistung. Sicherheitsfaktoren werden normalerweise auf Materialeigenschaften (z. B. Streuung von Eigenschaften, Verteilung im Raum, Streuung in der Lebensdauer), Randbedingungen (z. B. Beanspruchung, Umgebungs- und Betriebsparameter) und geometrische Variationen (z. B. Herstellungstoleranzen) angewendet. Die Wechselwirkung dieser Parameter kann jedoch nur durch einen probabilistischen Ansatz analysiert und berücksichtigt werden.
Dieser Artikel stellt die Strategie einer geometrischen Variationsanalyse und deren Ergebnis hinsichtlich des prognostizierbaren Verschleißverhaltens eines Gasturbinengehäuses vor. Hierbei steht die Aufgabe im Vordergrund, den Einfluss der geometrischen Streuung auf die Spannungen und die Lebensdauer zu quantifizieren. Das kann durch die Evaluierung von statistischen Eigenschaften und deren Übersetzung in Ausfallwahrscheinlichkeiten erreicht werden. Das generierte Wissen unterstützt dabei, Sicherheitsfaktoren und die Dauer zwischen Wartungsmaßnahmen anzupassen oder die Qualitätskontrolle für Fertigungstoleranzen zu verbessern.
Der Ablauf einer solchen Analyse beginnt mit der Bestimmung der realen geometrischen Abweichungen eines hergestellten Gehäuses im Vergleich zur CAD-Zielgeometrie. Eine genaue Messung der gefertigten Oberfläche kann durch Laserscans erfolgen. Durch das Scannen mehrerer Designs wird ein statistisches Modell für die geometrischen Variationen erstellt. Anschließend können mit Hilfe des Modells neue virtuelle Zufallsgeometrien erzeugt werden. Diese dienen als Eingabegrößen für eine CAE-Analyse. Letztendlich wird eine Art Monte-Carlo-Sampling verwendet, um die statistischen Eigenschaften von Antwortgrößen, wie z. B. Spannungs- oder Lebensdauerfaktoren, zu prognostizieren.
2 Arbeitsschritte
2.1 Messungen
Hierbei stellen die Oberflächenlaserscans bei einer Gehäusegröße von 4,9 m Durchmesser, 13,1 m Länge und 390 t Gewicht eine Herausforderung dar. Selbst moderne Scantechnologien erzeugen Datenmengen von mehr als 1 GB, um die Triangulation eines 180°- Scans zu speichern. Aufgrund der Größe des Objekts sind außerdem mehrere Scannerpositionen erforderlich. Zur Unterstützung der Messungen wurde das photogrammetrische System GOM Tripod in Kombination mit GOM ATOS Triple Scan eingesetzt (Bild 1).
Der Zeitraum zum Scannen der Turbine ist zwischen der Produktion und der Vorbereitung zur Lieferung sehr begrenzt. Deswegen können bei einigen Turbinengehäusen nur Teile der Oberfläche gescannt werden. Außerdem sind aufgrund der komplexen Geometrie einige Teile für Scangeräte gar nicht zugänglich. Daher muss die Triangulation nachträglich editiert werden, d. h. Vernetzungen bearbeiten, Simulationsmodelle vereinfachen, Fehlstellen beseitigen, Ausreißer bewerten und Anzahl der Triangulationen reduzieren (Bild 2).
Außerdem führen lange Lieferzeiten dazu, dass nur wenige Turbinengehäuse innerhalb einer akzeptablen Projektzeit gemessen werden können. Daher steht typischerweise für eine Analyse nur eine kleine Anzahl von Abtastwerten zur Verfügung. Indem die symmetrische Geometrie genutzt wird, kann man jedoch eine größere Anzahl von Werten virtuell generieren.
2.2 Statistisches Modell der geometrischen Toleranzen
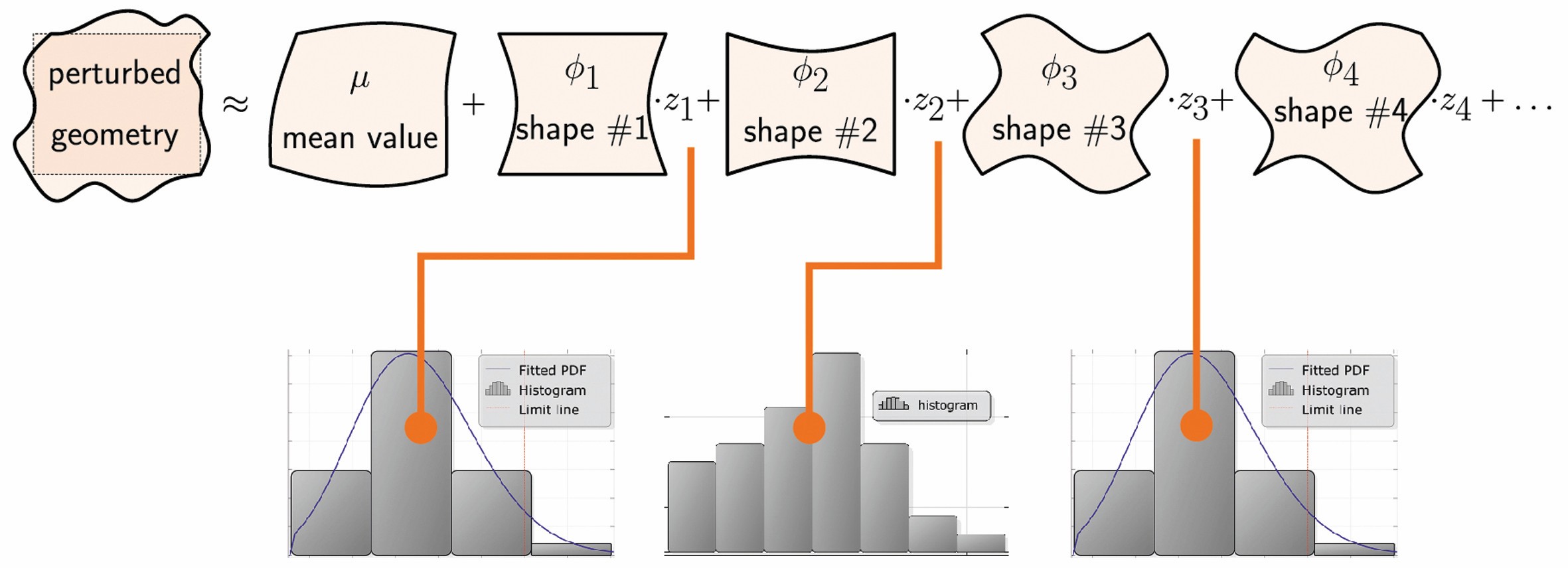
In einer Robustheitsanalyse werden neue virtuelle Geometrien zufällig generiert. Unter Verwendung von optiSLang werden statistische Eigenschaften (z. B. Verteilungstyp, Mittelwert, Standardabweichung, Korrelationen) einem kleinen Satz von Parametern zugewiesen. Diese Informationen werden verwendet, um die Eingabeparameter gemäß dem vordefinierten Schema zu variieren. Die statistischen Eigenschaften müssen aus der Analyse der Laserscans generiert werden. In diesem Projekt wurde ein Zufallsfeldmodell („statistisches Formmodell“) gewählt, um die geometrischen Variationen darzustellen (Bild 3).
Dabei werden statistische Parameter mit jedem einzelnen Punkt auf der Gehäuseoberfläche verknüpft. Dieses Vorgehen unterscheidet sich sehr von Ansätzen einer statistischen Beschreibung von CAD-Parametern. Das Zufallsfeldmodell ermöglicht hier eine größere Genauigkeit in der räumlichen Verteilung der Variationsmuster, da es an die FEM-Knoten und nicht nur an einige wenige Parameter gebunden ist. Die Parametrisierung kann automatisch durch eine Analyse der Messungen generiert werden.
Zuerst werden die Messungen in SoS importiert, indem die STL-Dateien, die die reale Bauteiloberfäche definieren, auf das undeformierte FEM-Netz projiziert werden. SoS bestimmt automatisch die geometrische Abweichung (gemessen senkrecht zur Oberfläche) für jeden FEM-Knoten zwischen jeder Messung und der Referenzgeometrie. Im nächsten Schritt wird eine statistische Analyse durchgeführt. Für jeden FEM-Knoten wird die mittlere Abweichung und die Größe der Abweichung um den Mittelwert (entspricht Standardabweichung) bestimmt. Aus dieser Analyse kann ein erster Hinweis abgeleitet werden, an welchen Stellen eine große Abweichung von der CAD-Geometrie zu erwarten ist (aus der Überprüfung des Mittelwertes) und an welchen Stellen aufgrund der natürlichen Streuungen im Produktionsprozess eine große Abweichung verursacht wird (Standardabweichung), siehe Bild 4.
Interessanterweise sind diese Punkte in unserem Projekt unterschiedlich. Mit mehr verfügbaren Proben hätte die SoS-Analyse noch erweitert werden können, um kritische Punkte durch Quantilwerte und Überschreitungswahrscheinlichkeiten zu lokalisieren. In jedem Fall hätte man die Statistiken hinsichtlich der Qualitätskontrolle gründlicher untersuchen können.
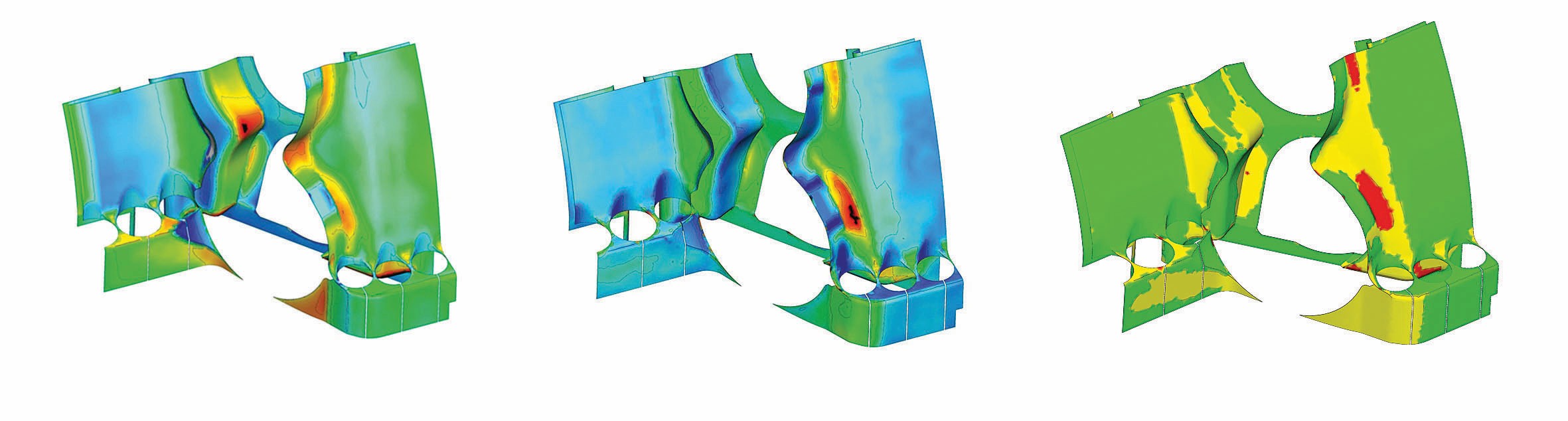
Bild 4 Statistische Analyse der gemessenen geometrischen Toleranzen. Links: mittlere Abweichung, Mitte: Standardabweichung der geometrischen Streuung, Rechts: Toleranzanalyse basierend auf 3-Sigma-Ebene (gelb und rot sind kritische Stellen). Bild: Siemens
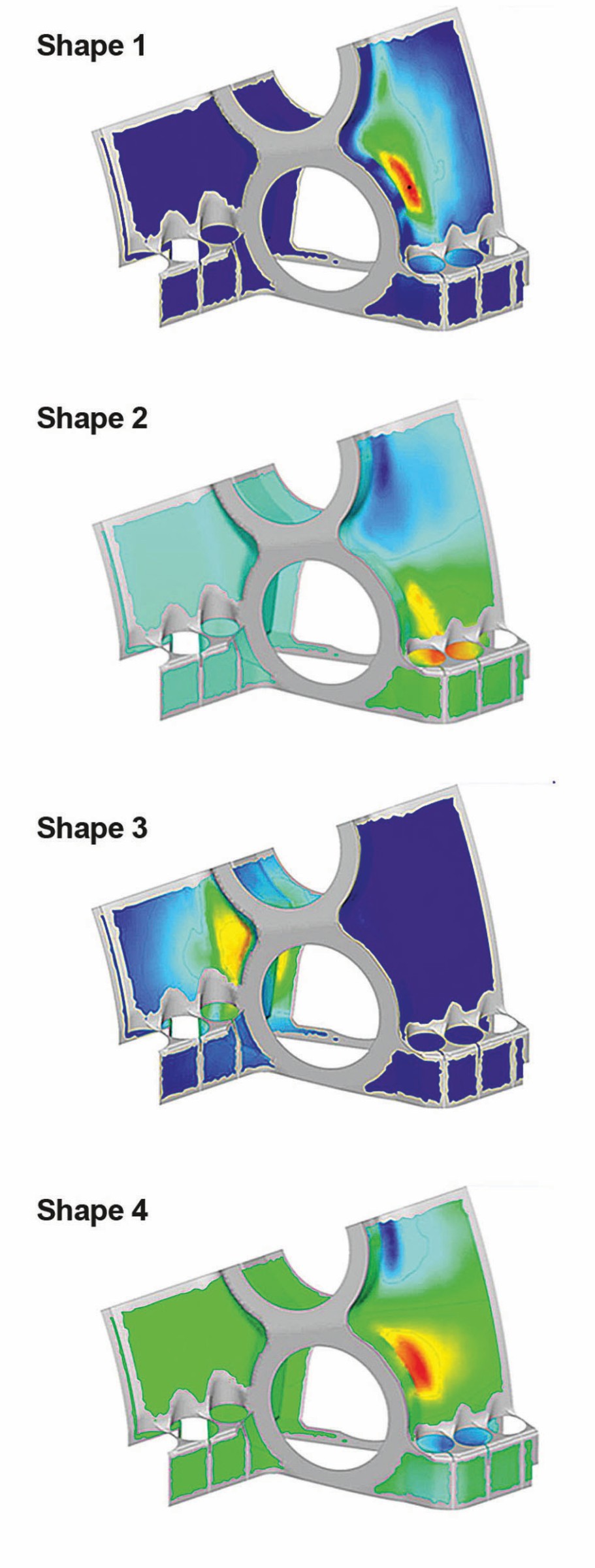
Der nächste Schritt ist die Erstellung eines statistischen Modells der geometrischen Abweichung. Das Zufallsfeldmodell besteht im Wesentlichen aus „Variationsmustern“ oder „Streuformen“. Mit einem vordefinierten, ausreichend großen Satz von Abtastwerten (z. B. 80) analysiert SoS zunächst die Daten auf korrelierte Variationsmuster (Bild 5).
Einmal identifiziert, kann SoS jede Messung durch eine Reihenentwicklung darstellen, wobei jede Variationsform um einen Koeffizienten skaliert und zum Mittelwert addiert wird. Normalerweise reichen nur wenige Variationsmuster (5 – 10) aus, um die realen Messungen mit hoher Genauigkeit darzustellen.
Da im Projekt nur sehr wenige Messungen verfügbar waren, wurden die Variationsmuster unter Verwendung analytischer Funktionen auf der Grundlage bestimmter technischer Annahmen (z. B. Korrelationslängenparameter) erzeugt. Wie die Messungen zeigten, ist das resultierende Modell ausreichend, um den Mittelwert und die Standardabweichung für jeden FEM-Knoten darzustellen. In SoS wird das als „synthetisches Zufallsfeldmodell“ bezeichnet.
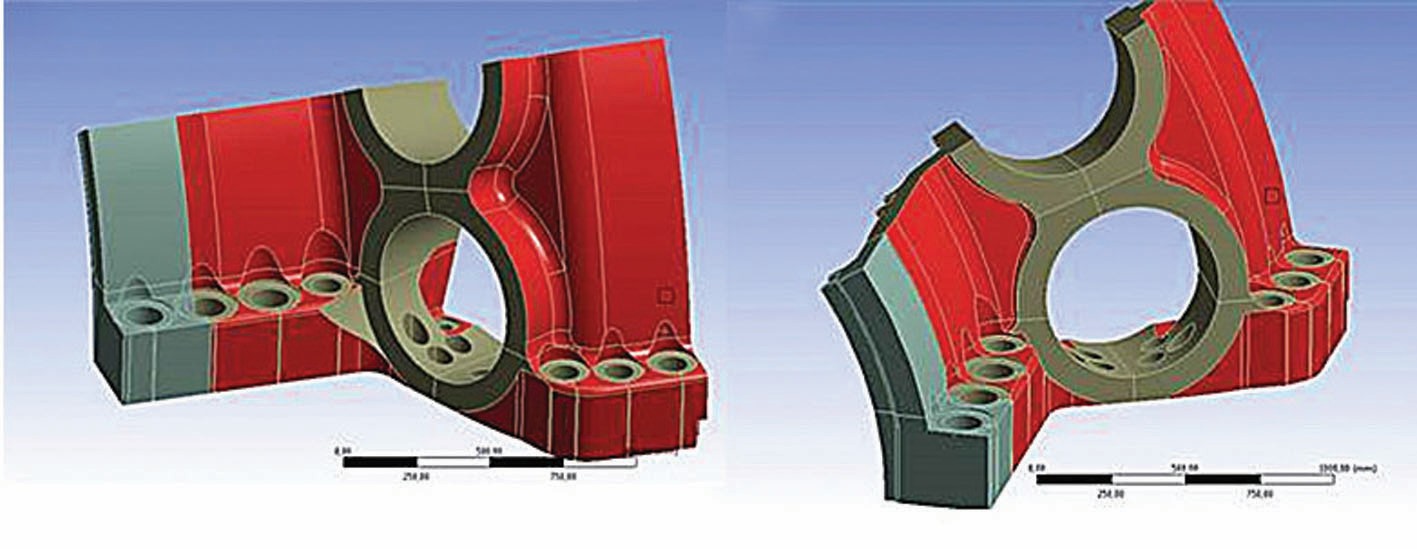
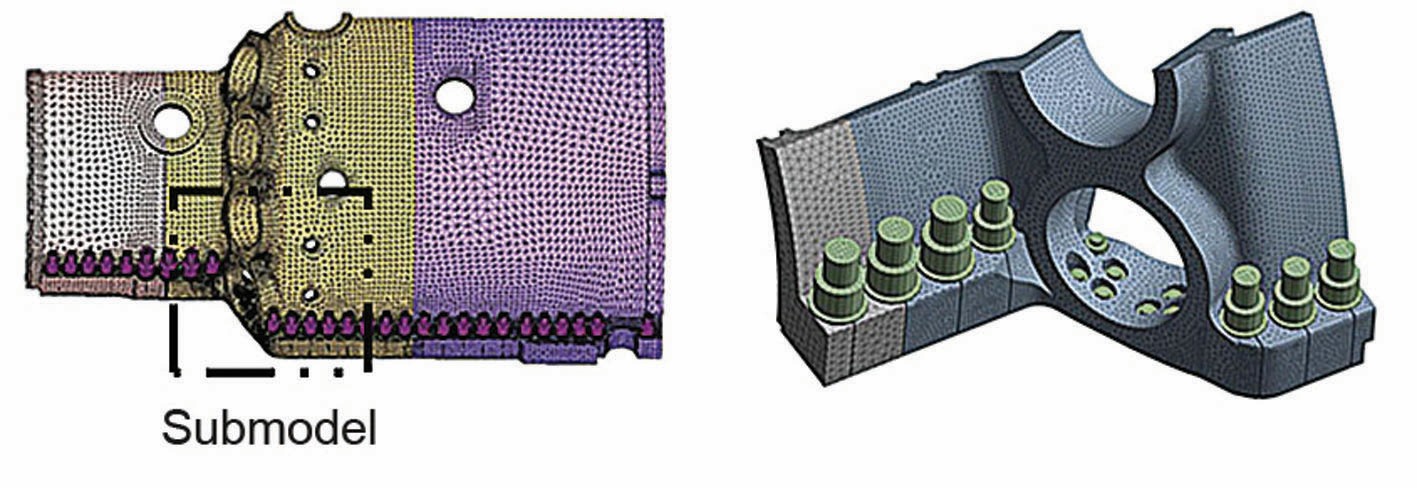
Das statistische Formmodell wird nicht für die gesamten Randbedingungen erstellt. Obwohl von Null verschiedene Abweichungen an allen Stellen der Oberfläche gemessen wurden, muss sich die Generierung von geometrischen Imperfektionen auf einzelne Oberflächenabschnitte beschränken. Einige Oberflächenteile werden nach dem Formen bearbeitet, z. B. werden Löcher gebohrt und geschliffen, um andere Bauteile, u.a. Schrauben, zu befestigen. Einige Oberflächenteile dürfen nicht verändert werden, um die numerische Stabilität des CAE-Modells, z. B. Kontaktgrenzen, sicherzustellen. Die variierten geometrischen Teile sind in Bild 6 dargestellt.
2.3 Numerisches Modell
Die Generierung des numerischen Modells erfolgte in Ansys Workbench. Zur Prognostizierung der räumlichen Verteilung von Temperatur und Spannungen, wurde ein semi-analytisches, thermisches Modell für die Gasströmung implementiert und mit einem transienten, thermomechanischen Modell gekoppelt. Die anschließende LCF-Analyse (Low Cycle Fatigue) wurde mit der Software Siemens GT durchgeführt. Das 3D-FEM-Modell umfasst Schraubkontakte und einen thermischen Transienten für die zeitabhängige Definition der Belastungsbedingungen.
Das ursprüngliche mechanische Modell für das 90°-Gehäuseteil besteht aus 840 k Knoten und 380 k Elementen. Die Gesamtrechenzeit für ein einzelnes Design erfordert mehr als 30 GB Speicherplatz und ungefähr drei Tage Rechenzeit mit einer HPC-Hardware. Daher ist der Lauf von z. B. 100 Proben in einem einfachen Versuchsaufbau einer Robustheitsanalyse innerhalb der Projektzeit nicht realisierbar.
Um die Zeit- und Speicheranforderungen zu verbessern, wurde nur ein Untermodell mit verbleibenden 240 k Knoten und 270 k Finiten Elementen berücksichtigt (Bild 7).
Die Hardware-Anforderungen konnten auf 7-GB-Festplattenspeicher und zwei Stunden Rechenzeit pro Sample reduziert werden.
Das numerische Modell wurde auf Basis des CAD-Geometriemodells erstellt. Sobald ein FEM-Netz verfügbar ist, kann das statistische Formmodell generiert werden. Die geometrischen Änderungen werden nicht auf das CAD-Modell angewendet, sondern auf die Koordinaten der FEM-Knoten. SoS ändert oder verkettet das FEM-Netz nicht, stattdessen „morpht“ es die Knoten des FEM-Netzes in die gewünschte Form. Bevor das Ansys Workbench-Modell von optiSLang ausgewertet wird, bereitet SoS APDL-Makros im Ansys Workbench-Modellordner vor, die in Ansys Mechanical als Anweisung für die Geometrieänderung verwendet werden. SoS nutzt dafür Stabilisierungs- und Glättungsalgorithmen, die die Stabilität und Berechenbarkeit des veränderten FEM-Netzes gewährleisten. Vor der Durchführung der Robustheitsanalyse wird ein Testlauf der Solver-Kette unter Verwendung der Mittelwertgeometrie durchgeführt.
2.4 Robustheitsanalyse und Ergebnisse
Mit Hilfe der Robustheitsanalyse sollen folgende Fragen beantwortet werden:
Gibt es Abweichungen in der Spannungsverteilung oder der Lebensdauer zwischen der realen Geometrie und der Referenzgeometrie?
Gibt es einen signifikanten Einfluss auf das Spannungsverhalten und die Lebensdauer, wenn die geometrische Streuung berücksichtigt wird? Wie groß ist der Einfluss?
Die erste Frage kann beantwortet werden, indem jede Messung in das CAE-Modell übertragen oder einfach die mittlere Geometrie berechnet wird. Die zweite Frage erfordert eine stochastische Toleranzanalyse. Hierbei wird ein virtuelles Design of Experiments (DOE) erstellt und ausgewertet (Bild 8).
Dies beinhaltet eine Variation der Zufallsfeldparameter gemäß ihren statistischen Verteilungen. SoS vereinfacht die Auswahl durch die Annahme von unkorrelierten Standard-Normalvariablen.
Die Ergebnisse der CAE-Analyse (Temperatur, Spannungen, Lebensdauer usw.) können entweder in optiSLang (z. B. durch ihre Maximalwerte) oder in SoS analysiert werden. Dazu werden die Ansys RST-Dateien von SoS neu bewertet (Bilder 9, 10).
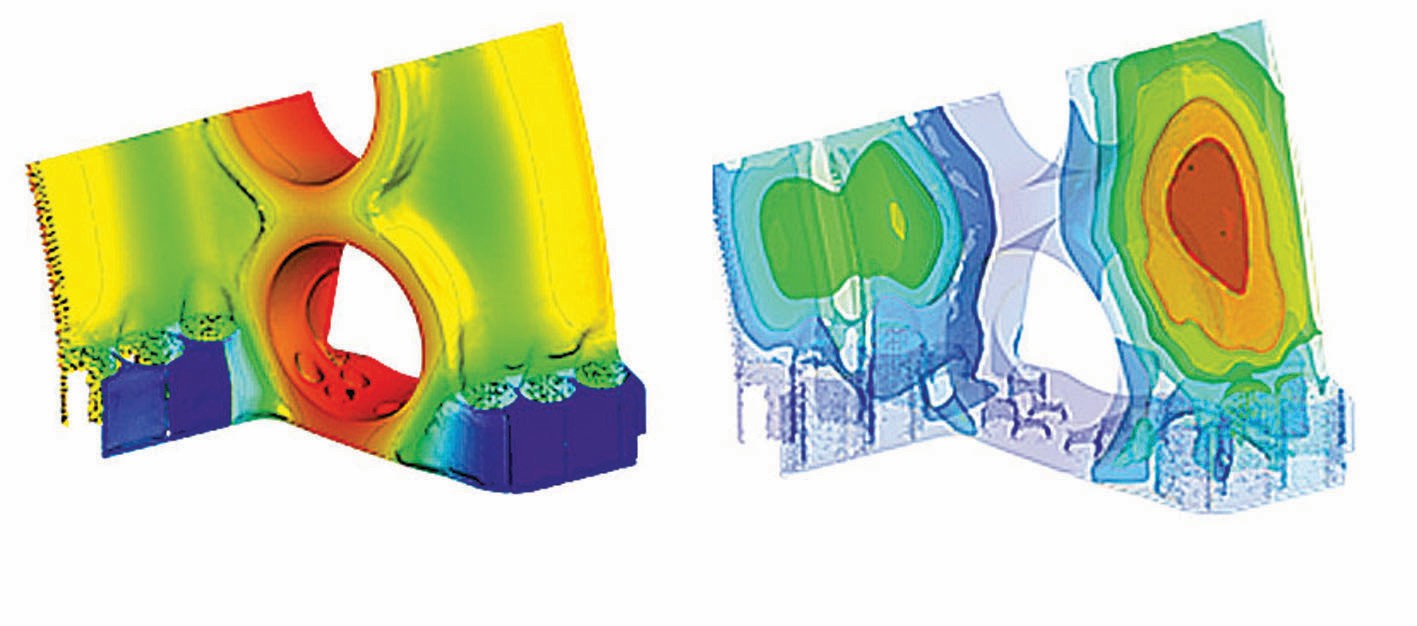
Bild 9 Statistische Analyse des resultierenden Temperaturfeldes. Links: Mittelwert, Rechts: Standardabweichung. Bild: Siemens

Bild 10 Statistische Analyse des resultierenden von Mises-Spannungsfeldes. Links: Mittelwert. Rechts: Standardabweichung. Bild: Siemens
Danach wird eine statistische Analyse für die Ergebniswerte durchgeführt. Die Spannungen können beispielsweise mit kritischen Grenzwerten für unterschiedliche Sicherheitsstufen (Überschreitungswahrscheinlichkeiten) verglichen werden. Außerdem kann man das Auftreten von kritischen Spannungen leicht identifizieren und lokalisieren.
Eine Ausfallwahrscheinlichkeit wurde in diesem Projekt nicht analysiert, da die Genauigkeit des statistischen Modells aufgrund der geringen Anzahl von Messungen nicht ausreicht. Weiterführend kann eine Sensitivitätsanalyse mit dem Field Metamodel of Optimal Prognosis (FMOP) durchgeführt werden. Das FMOP ordnet die Sensitivitäten der Spannungen oder Temperaturen jedem FEM-Knoten für die jeweiligen Eingangsparameter zu (Bild 11).
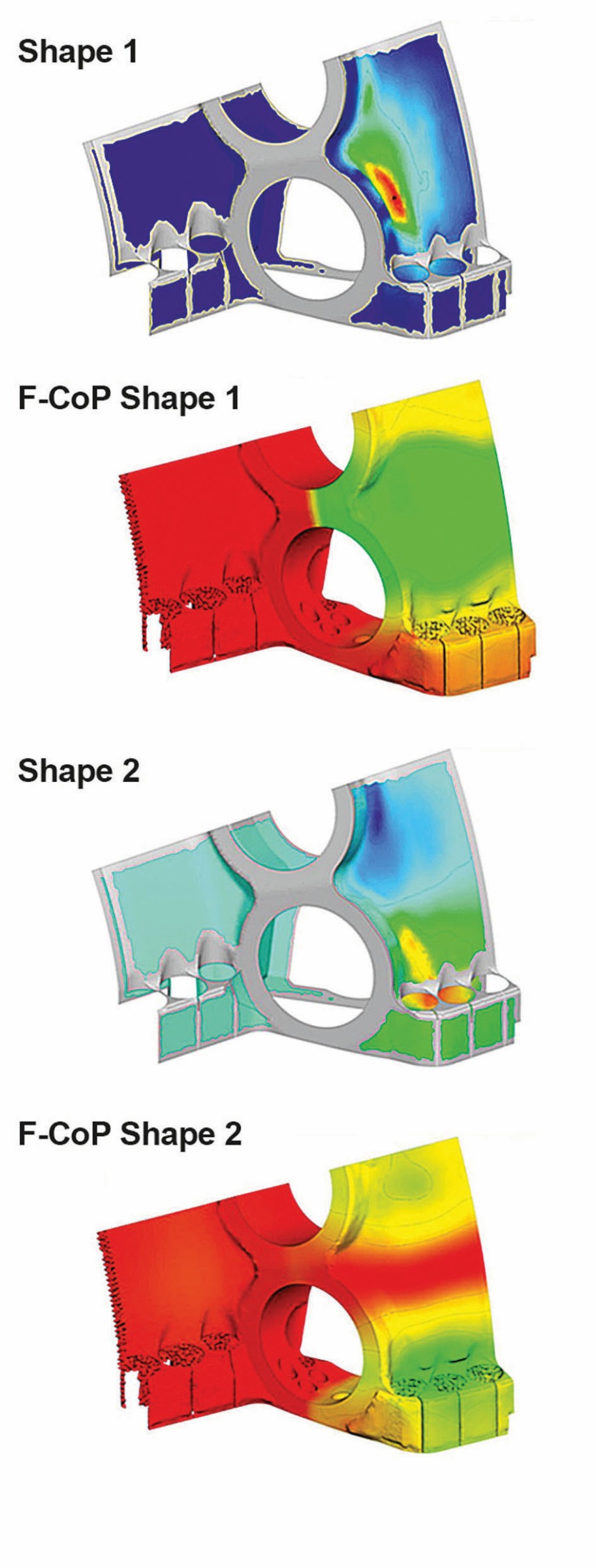
Bild 11 Sensitivitätsanalyse des Temperaturfeldes mit FMOP – das dominanteste geometrische Variationsmuster für resultierende Temperaturänderungen mit der korrespondierenden Sensitivität (F-CoP) der Temperatur in Bezug auf die geometrischen Variationsmuster. Bild: Siemens
In dieser Analyse repräsentiert jeder Eingangsparameter ein bestimmtes Variationsmuster. Diese Muster zeigen an, welche geometrische Variationsform für die Temperatur oder Spannung an kritischen Stellen relevant ist. Das Ergebnis bewertet darüber hinaus die Qualitätskriterien für geometrische Fertigungstoleranzen gegenüber den jeweiligen Variationsformen.
3 Software und Methodik
Liste der verwendeten Software und der speziellen Funktionen im Workflow:
optiSLang
- Management und Automatisierung des Workflows
- Generierung von Zufallswertparametern und DOE
- Analyse von skalaren Antwortgrößen
Ansys
- Erstellung des thermomechanischen Modells
Siemens GT
- Berechnungsprogramm für Low Cycle Fatigue
Statistics on Structures
- Statistische Analysen der Messungen
- Generierung neuer Zufallsgeometrien und Implementierung in den CAE-Prozess
- Statistische Analysen der FEM-Ergebnisse in 3D
- Sensitivitätsanalyse von FEM-Ergebnissen mit FMOP in 3D
Der Beitrag beruht auf dem Vortrag „Untersuchung der Lebensdauer von Gasturbinengehäusen unter Berücksichtigung geometrischer Streuungen”, der auf den Weimarer Optimierungs- und Stochastiktagen vom 1.-2. Juni 2017 präsentiert wurde.
Uwe Lohse
Siemens AG, Power and Gas Division Products Design and Component PG PR R&D GTM EE DC, Mellinghofer Str. 55, 45473 Mülheim a. d. Ruhr
www.siemens.com
Holger Schulze Spüntrup
ITB Ingenieurges. für techn. Berechnungen mbH, Europaplatz 7, 44269 Dortmund
www.itb-fem.d/
Sebastian Wolff
Dynardo Austria GmbH, Wagenseilgasse 14, A- 1120 Wien
www.dynardo.de