Das MONTE-CARLO-Experiment
Das Monte-Carlo-Experiment ermöglicht die numerische Simulation von statistischen Grundgesamtheiten und somit auch die Generierung von Festigkeitswerten für eine genau definierte Population von Druckgefäßen. In diesem Beitrag wird möglichst nachvollziehbar gezeigt, wie Werte generiert, Stichproben gezogen und ausgewertet werden. Auf dieser Basis wird auch gezeigt, wie die Wahrscheinlichkeit ermittelt wird, mit der Stichproben aus simulierten Populationen das Zulassungskriterium „Mindestberstdruck“ bestehen.

Quelle: BAM
Die Bundesanstalt für Materialforschung und -prüfung (BAM) entwickelt und verbesserst seit über 10 Jahren statistische Methoden zur probabilistischen Sicherheitsbewertung von Composite-Druckgasspeichern (s. [1]) wie diese insbesondere für die Speicherung von Wasserstoff eingesetzt werden (vergl. Bild 1).Ziel dieser u. a. in [2-6] dargestellten Arbeit ist deren sicherer Betrieb und ein die Gestaltung möglichst wenig limitierender Zulassungsansatz. Um die Wirksamkeit dieses Bewertungsansatzes zu überprüfen, wird seit 5 Jahren in zunehmendem Maße das Monte-Carlo-Experiment zur Simulation des Verhaltens von Populationen eingesetzt. Mithilfe dieser Monte-Carlo-Simulation (MCS) (vergl. auch Kap. 5.2.2 in [7]) ist es möglich Akzeptanzkriterien im Hinblick auf die verschiedenen Berstfestigkeiten [8,9] oder Lastwechselfestigkeiten [10] von unterschiedlichsten Grundgesamtheiten systematisch zu untersuchen. Mit diesem Werkzeug lassen sich die Mindestanforderungen in Vorschriften und Regelwerke auf ihre Wirkung hin untersuchen und auch optimieren.
Das Prinzip der Monte-Carlo-Simulation
Die Monte-Carlo-Simulation (MCS) basiert auf Wahrscheinlichkeitsrechnung und Statistik. Für das Verständnis der Ergebnisse aus diesen Simulationen ist es vorteilhaft, das Herangehen zunächst mit einem einfachen und nachvollziehbaren Beispiel schrittweise aufzubauen. Das Prinzip der MCS kann durch ein Experiment zur Approximation der Zahl p („Pi“) beschrieben werden. Unter der Bezeichnung „Approximation von p“ wird hier die immer weiter verfeinerte Abschätzung von p über eine geometrische Betrachtung mithilfe statistischer Mittel verstanden.
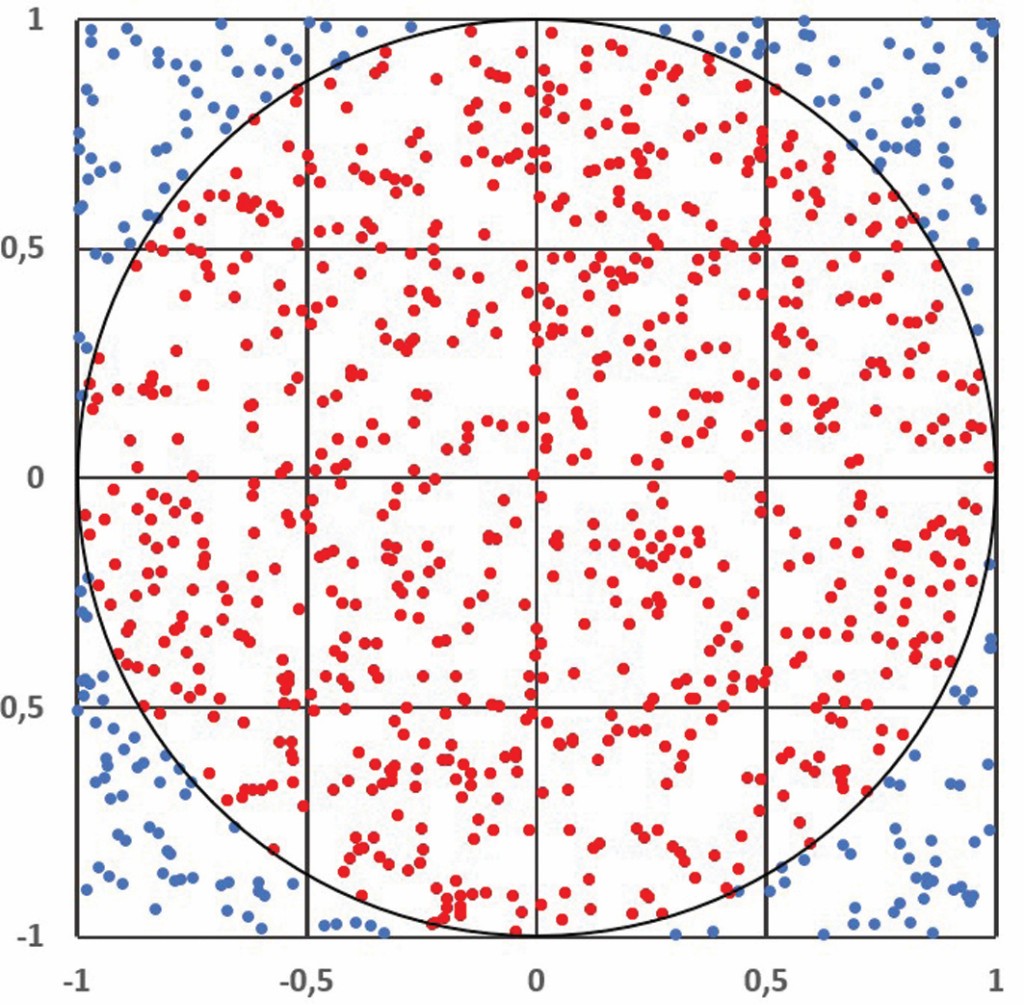
Bild 2 zeigt ein Einheitsquadrat mit eingeschlossenem Einheitskreis.
Darin sind aus zufällig und unabhängig generierten Zahlenwerten Punkte im Diagramm abgebildet. Es wird erwartet, dass sich die Anzahl der generierten Punkte im Einheitskreis (PK) in Relation zur Anzahl der Punkte (PQ) im Einheitsquadrat genauso verhält wie das Verhältnis der zugehörigen Flächen AK und AQ. D. h.:
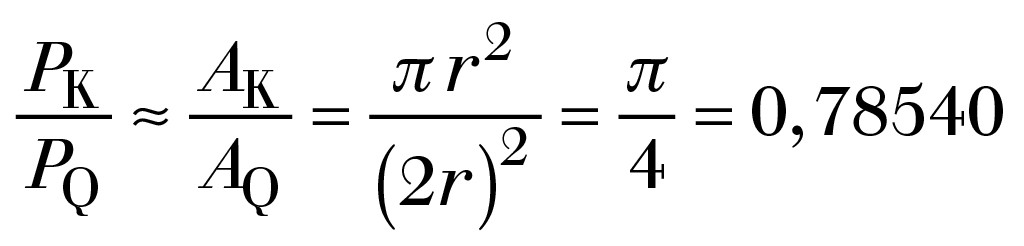
Aus Gründen der Anschaulichkeit ist dies in Bild 2 anhand von lediglich 1 000 Punkten dargestellt. Das Ergebnis dieses Experimentes ist abhängig von der betrachteten Anzahl der Punkte in Tabelle 1.
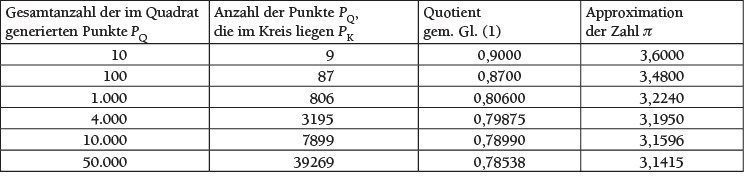
Tabelle Annäherung an die Zahl Pi.
Aus den Zahlenergebnissen der Tabelle 1 ist ersichtlich, wie durch zufällige und unabhängige Anordnung von Punkten im Bild 2 eine gute Annäherung an die Zahl p mit Experimenten der MCS statistisch ermittelt werden kann. Zudem ist durch die Zahlenreihen im gewählten Experiment veranschaulicht, dass je höher die Anzahl der generierten Punkte ist, desto besser wird die Approximation. Die Ergebnisse aus der Reihe von Simulationen konvergieren zur exakten Lösung.
Einstieg in die Programmierung der Monte-Carlo-Simulation auf Basis der Polarmethode
Die MCS basiert auf Zufallszahlen und damit auf der Anwendung eines Zufallsgenerators. Als Beispiel für eine mögliche Vorgehensweise für eine normalverteilte MCS wird nachfolgend die Polar-Methode gezeigt.
Die Polarmethode von George MARSAGLIA und Thomas A. BRAY ist ein mögliches Verfahren zur Erzeugung normalverteilter Zufallszahlen und kann als Zufallszahlengenerator für erforderliche Basisdaten in der MCS dienen. Die Polarmethode geht zurück auf den Box-Müller Algorithmus zur Erzeugung normalverteilter Zufallsgrößen. Bei diesem Algorithmus werden euklidische Koordinaten verwendet.
In der Polarmethode geht man von zufälligen Punkten in der Ebene aus, die in einem gedachten Einheitskreis r = 1 etwa gleichverteilt angeordnet sind. Die Koordinaten für die Punkte werden aus Zufallszahlen generiert.
Das nachfolgende Beispiel ist für eine kleine Grundgesamtheit < 100 ausgeführt.
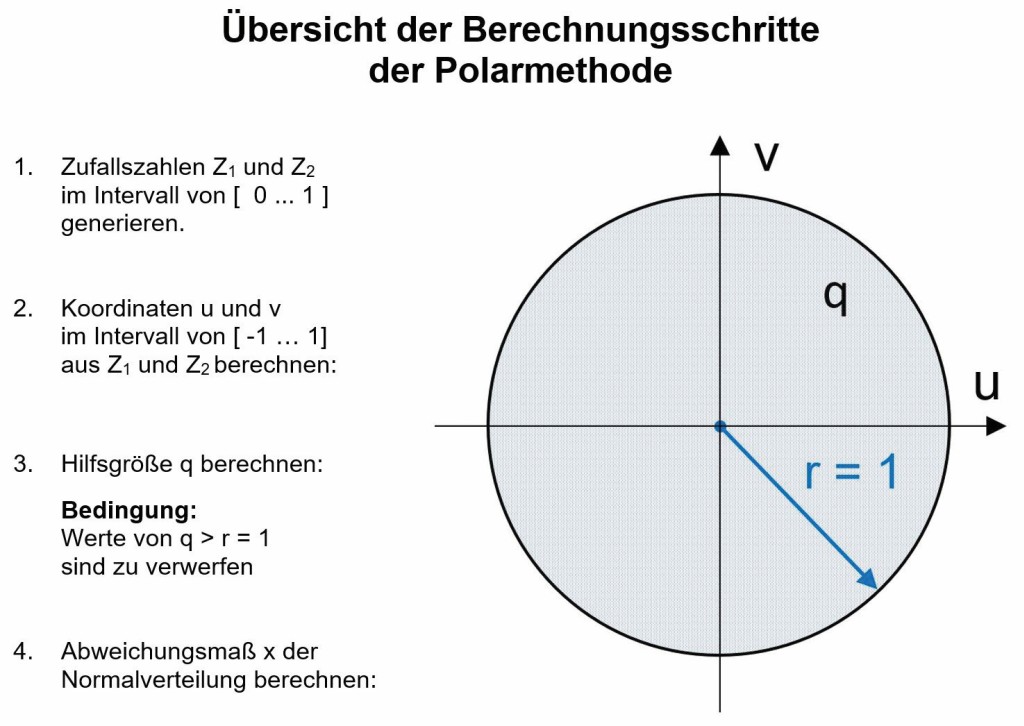
Beschreibung der Abfolge für das Generieren von Zufallszahlen durch Anwendung der Polarmethode (s. Bild 3)
In der Polarmethode sind gemäß [8] für jedes simulierte Individuum je zwei Zufallszahlen Z1, Z2 mittels eines Zufallszahlengenerators im Intervall von [0… 1] unabhängig zu erzeugen. Die so erzeugten Werte sind in den nachfolgenden Bildern als Punkte dargestellt.1)
Im nächsten Schritt sind die Werte für die Koordinaten im Einheitskreis u und v aus den zuvor erzeugten paarweisen Zufallszahlen nach den folgenden Gleichungen in das Intervall von [ -1 … 1] zu transformieren.
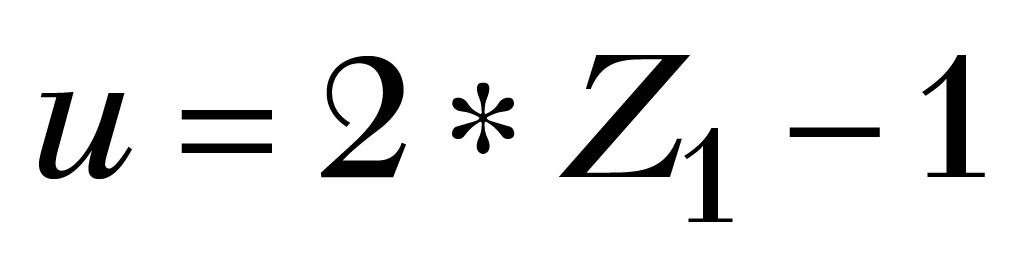
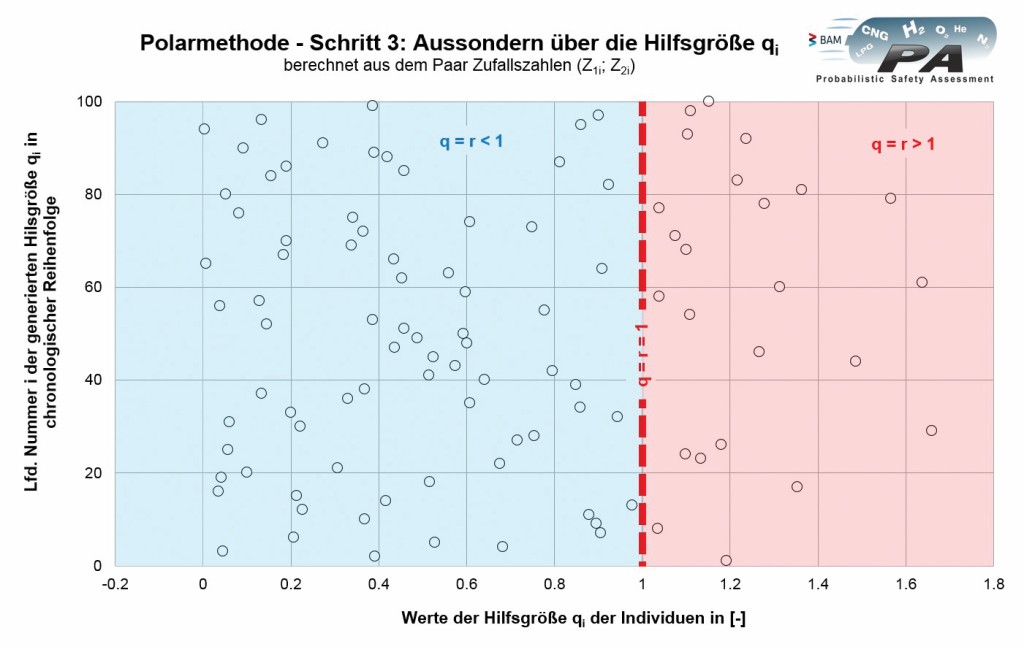
In einem dritten Schritt ist der Wert der Hilfsgröße q für jedes Individuum i zu berechnen:
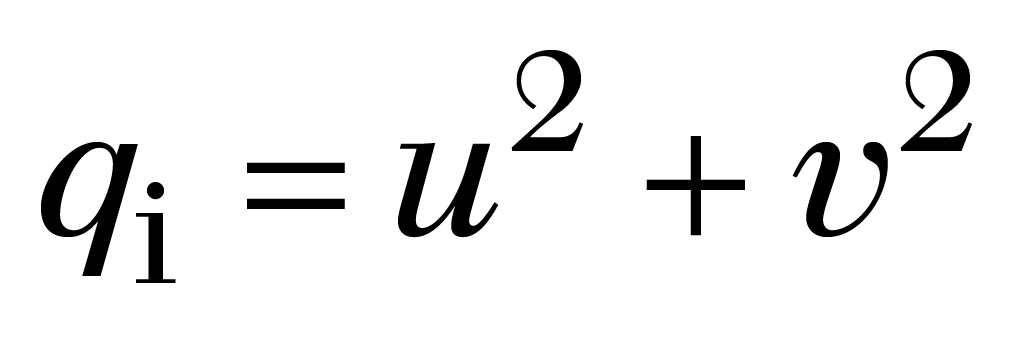
Ergeben sich dabei Zahlenwerte für q, für die gilt q = r > 1, müssen diese Individuen verworfen werden. Die Ergebnisse für qi sind im Bild 4 dargestellt.
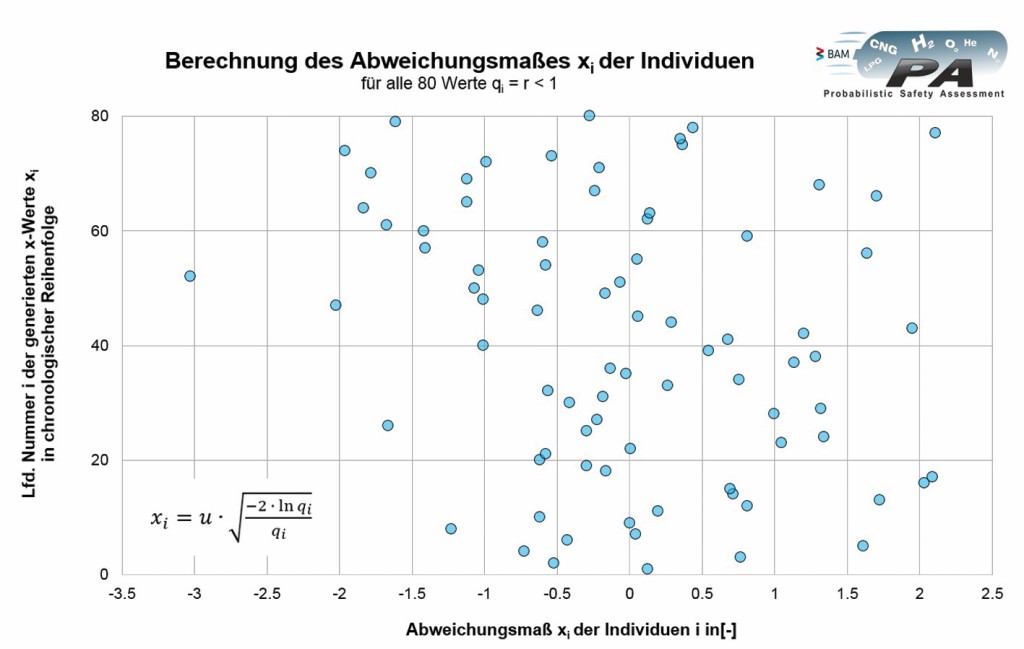
In einem vierten, in Bild 3 sichtbaren Schritt werden die Werte für das Abweichungsmaß x der Normalverteilung berechnet:
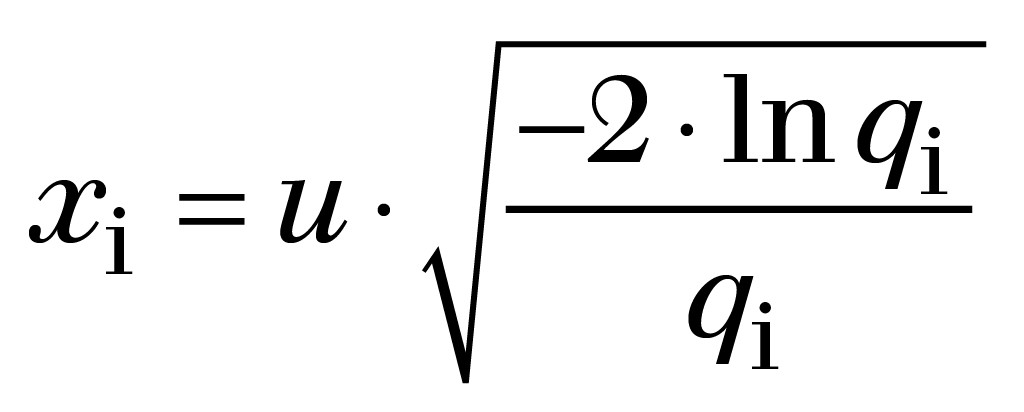
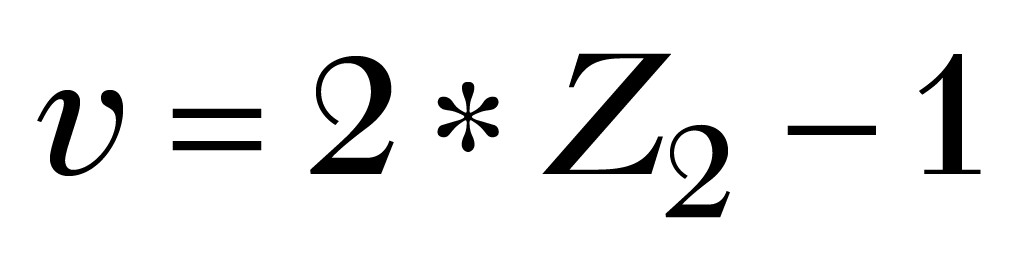
Damit erhält man die in Bild 5 dargestellten Werte. Jeder Punkt steht für ein Individuum bzw. die betrachtete Eigenschaft des Individuums. Die Menge aller Punkte zeigt die ganze generierte Population aus Individuen.
Durch Anwendung der Bedingung im dritten Berechnungsschritt werden die Zahlenwerte von q bzw. die Individuen i verworfen, die außerhalb des Einheitskreises liegen (q = r > 1). Sofern nicht Ersatzwerte nachgeneriert werden, reduziert sich dadurch die Anzahl der simulierten Individuen im weiteren Rechengang der Polarmethode entsprechend.
Normalverteilte Eigenschaften von Individuen lassen sich nicht nur mit der Polarmethode erzeugen. Inzwischen kann davon ausgegangen werden, dass übliche Programme entsprechende Generatoren für Zufallszahlen enthalten, die eine Wertewolke wie in Bild 5 dargestellt, automatisch generieren.
Generierung von Populationen mithilfe der Monte-Carlo-Simulation
Im Folgenden werden die generierten Zufallszahlen verwendet, um die Eigenschaft „Berstfestigkeit“ einer generierten Population von Druckbehältern aus Verbundwerkstoffen (Composite-Speichern) zu simulieren, wie diese für die Speicherung von Wasserstoff in Fahrzeugen oder auf Trailerfahrzeugen eingesetzt werden.
Hierbei sind die Eigenschaften der Population durch die Parameter „Mittelwert“ aller Berstfestigkeiten Wμ und der „Standardabweichung“ dieser Berstfestigkeiten Ws beschrieben. Genauer gesagt, sind diese zentralen Eigenschaften W der Gesamtpopulation wie auch die vergleichbar nachfolgend verwendeten Eigenschaften von Stichproben auf den maximalen Betriebsdruck bezogen. Durch diese Normierung erhält man einen universellen Zahlenwert, der in einem speziell hierfür aufbereiteten, normiertem Arbeitsdiagramm nach Kap.3.1 aus [6] einfach dargestellt und bewertet werden kann.
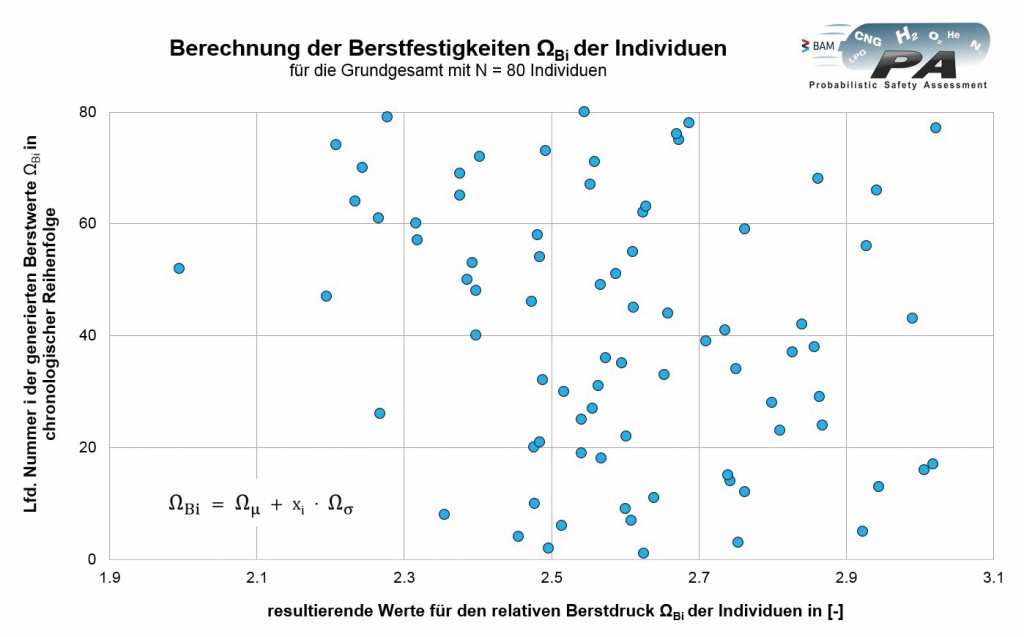
Um die hier betrachtete Berstfestigkeit WBi eines Individuums i zu erhalten, wird das generierte Abweichungsmaß eines Individuums mit den angenommenen Eigenschaften der Gesamtpopulation (vergl. Kap. 3.4 aus [6]) kombiniert (Bild 6):
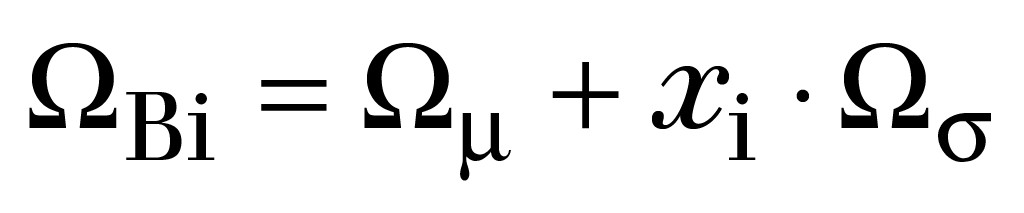
Das folgende Beispiel basiert auf nachfolgenden Vorgaben für die Population:
Wμ=2,6 für den „mittleren Berstdruck“ und
Ws= 0,2 für die „Standardabweichung“
Überprüfung der statistischen Verteilung der generierten Einzelwerte für die Berstfestigkeit
Grundsätzlich ist es immer sinnvoll zu prüfen, ob die angenommene Verteilung (hier GAUSSsche Normalverteilung2)) auch tatsächlich generiert wurde (vergl. [11]). Mit einem einfachen Test lässt sich nicht nur die Güte der Werte erkennen, sondern auch, ob in der Generierung ein „handwerklicher“ Fehler gemacht wurde.
Druckbehälter sind für einen garantierten Mindestberstdruck ausgelegt und gefertigt. Tatsächlich schwanken die realen Berstdrücke aber erheblich, sodass auch nie ausgeschlossen werden kann, dass der garantierte Mindestberstwert von wenigen Individuen unterschritten wird.
Zur Aufbereitung der Werte WBi für die Darstellung im GAUSSschen Wahrscheinlichkeitsnetz wird hier auf Kap. 3.2.1 aus [6] verwiesen.
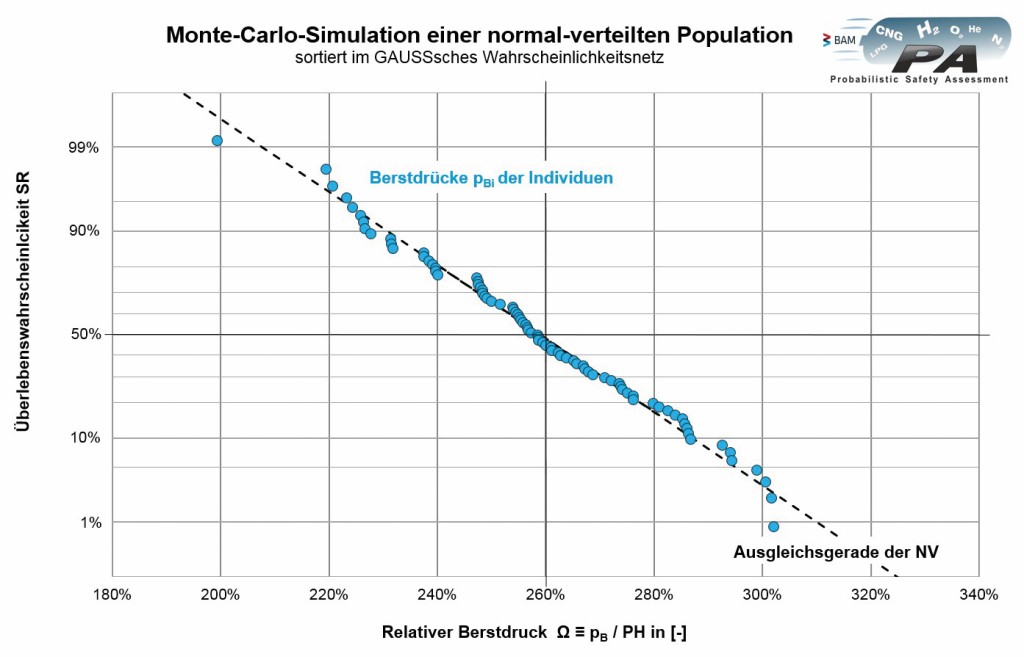
Im Bild 7 ist der Vergleich der generierten Festigkeitswerte (Punkte) mit einer idealen Normalverteilung (Gerade) dargestellt.
Da alle Werte eng um die Gerade streuen, liegt kein Hinweis darauf vor, dass die generierten Werte nicht normalverteilt wären oder die Auswertung der Population nicht zu den Individuen passen würde. Die im Bild 7 unterbrochen gezeigte Linie stellt die Ausgleichsgerade dar. Der Mittelwert der Population bzw. Grundgesamtheit mit einer Mächtigkeit Q von 80 Werten ist durch den Ordinatenwert der Ausgleichsgeraden bei 50 % Überlebenswahrscheinlichkeit SR gegeben. Der Gradient der Ausgleichsgeraden beschreibt die Standardabweichung des relativen Berstdrucks der generierten Population.
Generierung von Stichproben mit der Monte-Carlo-Simulation
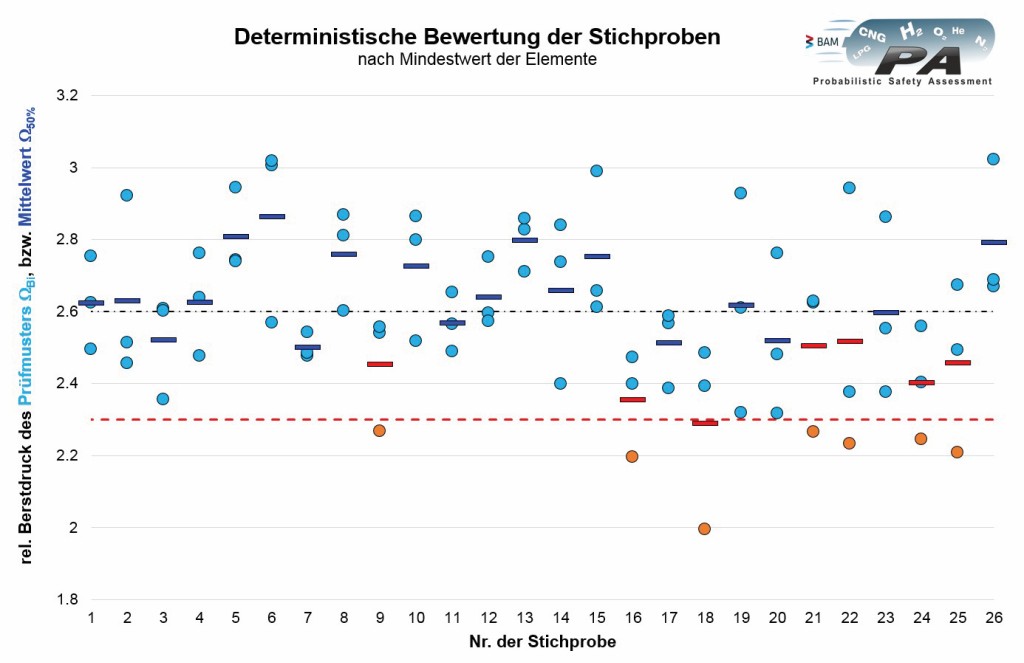
Möchte man reale Prüfergebnisse simulieren, muss man von einer Population (Grundgesamtheit) ausgehend die relevanten Stichproben ziehen. Dies lässt sich gut mit der MCS simulieren. Hierzu wird mit einem erneuten Zufallsprinzip oder unter Ausnutzung der zufällig entstandenen Chronologie bei der Generierung der Grundgesamtheit die jeweils vorgegebene Anzahl n von Prüfmustern in einer Stichprobe „gezogen“ und statistisch bewertet. Dies ist für das in Bild 8 gewählte Datenbeispiel für eine Stichprobengröße von n = 3 dargestellt.
Die drei Einzelwerte der Stichproben sind jeweils über der laufenden Nummer der Stichprobe dargestellt.
Im nächsten Schritt nimmt man nun ein klassisches Akzeptanzkriterium in die Betrachtung hinzu. Es wird für den relativen Berstdruck jedes Individuums ein Mindestwert in Höhe des 2,3-fachen des maximal auftretenden Betriebsdruckes gefordert. Dies entspricht einem Mindestwert des doppelten Prüfdrucks für Druckgefäße nach [12], wenn der maximale Betriebsdruck und damit der Gasdruck bei 65 °C einen Wert von 85 % des Prüfdruckes nicht überschreitet, wie dies z. B. für Wasserstoff der Fall ist. Alle Einzelwerte aus den Stichproben, die den Mindestwert erfüllen, sind in Bild 8 blau dargestellt (bestanden), Einzelwerte unter dem Mindestwert, sind orange dargestellt (durchgefallen). Die zugehörigen Mittelwerte einer Stichprobe sind mit einem horizontalen Balken gekennzeichnet. Der angestrebte Gesamtdurchschnitt von 2.6 ist ergänzt. Auf diese Art und Weise können auch die Akzeptanzkriterien für die Berstprüfung verschiedener Regelwerke betrachtet werden [9].
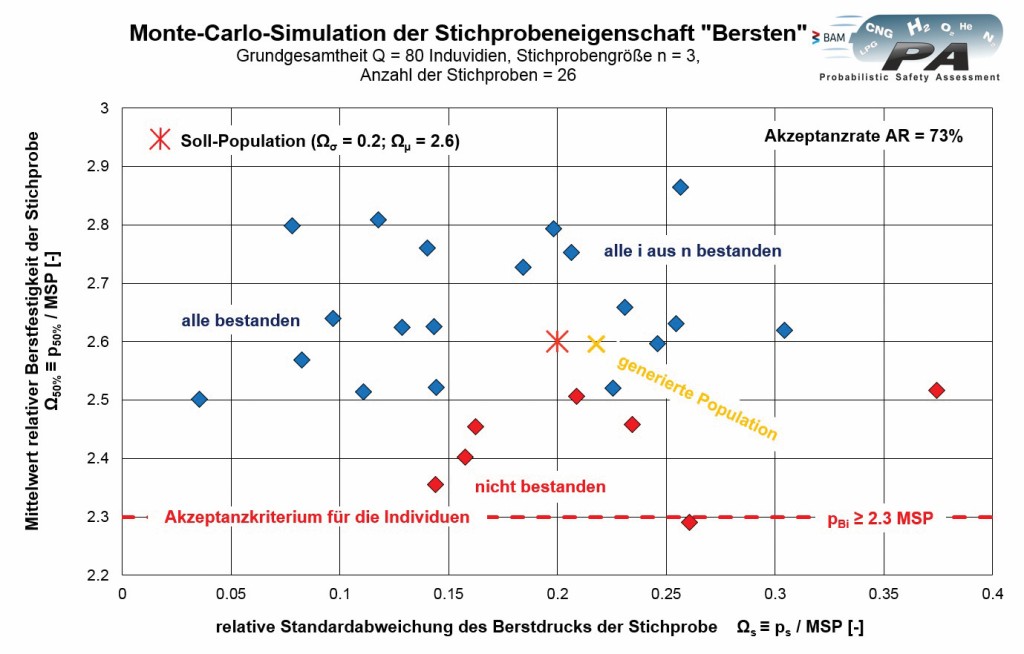
Bild 9 zeigt das in nach Kap.3.1 aus [6] eingeführte Arbeitsdiagramm zur Darstellung der Eigenschaft „Berstfestigkeit“.
Aus der Zusammenfassung der Werte von Berst-Eigenschaften von hier je 3 Einzelbehältern in einer Stichprobe können Mittelwert und Standardabweichung der jeweiligen Stichprobe berechnet werden. Somit können die simulierten Stichprobeneigenschaften als jeweils ein Punkt im Diagramm dargestellt werden. Aus den generierten 80 Individuen lassen sich insgesamt 26 Stichproben a 3 Individuen ziehen und statistisch bewerten.
Erfüllen alle Individuen einer Stichprobe diesen deterministischen Mindestwert nach Bild 8, ist der Punkt, der die gesamte Stichprobe in Bild 9 repräsentiert, blau dargestellt. Enthält die Stichprobe ein oder mehrere Individuen, die die geforderte Festigkeit nicht erreichen, ist die Stichprobe rot dargestellt.
Setzt man nun die Anzahl der blauen Punkte (19 Stichproben mit deterministisch hinreichenden Individuen) in Relation zur Gesamtzahl der Stichproben (26), erhält man die Akzeptanzrate. Dies ist die Wahrscheinlichkeit, dass aus einer gezogenen Stichprobe alle Elemente die Prüfung bestehen. Die Akzeptanzrate für die hier simulierte Grundgesamtheit (Ws = 0,2; Wμ = 2,6) beträgt somit 73 %.
Nimmt man noch die probabilistische Bewertung – wie in [6,7,9,10] gezeigt – hinzu, können unterschiedliche Auswirkungen von Prüfkriterien Bersten [9] und Lastwechseln [10] entsprechender Regelwerke für Zulassung von Baumustern von Composite-Druckbehältern auf ihre Wirksamkeit bzgl. der Steuerung der Ausfallwahrscheinlichkeit untersucht werden.
Natürlich können nach dem hier gezeigten Ansatz bzgl. Verteilung und Umfang3) unterschiedlichste Grundgesamtheiten auf verschiedene Eigenschaften hin untersucht werden. Auch kann der Einfluss der gewählten Stichprobengröße n (= 3..7..11..) oder die Reihenfolge bei der Zusammenstellung und Gruppierung von Stichproben simuliert werden.
Fazit
Die Monte-Carlo-Simulation ist eine geeignete Methode, um Festigkeitseigenschaften wie z. B. Berstdruck, oder auch die Lastwechselfestigkeit von ganzen Populationen von Druckbehältern zu simulieren.
Diese Simulation von Druckbehälterpopulationen und /oder Stichproben aus diesen Populationen ermöglicht Analysen, die sonst wegen ihres sehr großen zeitlichen oder wirtschaftlichen Aufwandes nicht möglich wären.
Dies erlaubt wiederum die systematische Analyse der Wirksamkeit von deterministischen Mindestanforderungen und die Optimierung entsprechender Zulassungsvorschriften. TS713
1)Beispielweise kann in MS-Excel hierzu die Funktion: „Zufallszahl()“ genutzt werden.
2)Messwerte vieler natur-, wirtschafts- und ingenieurwissenschaftlicher Vorgänge lassen sich durch die Normalverteilung (NV) in sehr guter Näherung beschreiben. Eine Reihe von Versuchsreihen an der BAM haben gezeigt, dass die Berstfestigkeit der meisten Baumuster, zumindest im Neuzustand durch die NV beschrieben werden können [9]. Es gibt aber auch wenige, noch unveröffentlichte Gegenbeispiele.
3)In den Anwendungen der MCS zur Betrachtung großer Grundgesamtheiten aus ggf. vielen Millionen Individuen, ist es im Gegensatz zum gezeigten, übersichtlichen Beispiel üblich, auf statistische Aufgaben ausgerichtete Softwarepakete einzusetzen.
Literatur
[1] Mair, G. W. ; Lau, M.: Beitrag zur Beurteilung der ermüdungsbedingten Ausfallsicherheit von Composite-Druckgefäßen. Technische Überwachung (TÜ) Bd. 49 (2008), Nr. 11/12 (Nov./Dez.), S. 33 – 38. ISSN 1434–9728
[2] Mair, G. W.; Scherer; F.: Statistische Bewertung von Prüfergebnissen zur Restfestigkeitsbetrachtung von Composite-Druckgefäßen. TS 3 (2013) Nr. 7/8, S. 41-49
[3] Mair, G. W.; Hoffmann, M.: Baumusterprüfung von Composite-Druckgefäßen, Probabilistische Betrachtung der Mindestberstanforderung nach Norm. TS 3 (2013) Nr. 11/12, S. 48-54
[4] Mair, G. W.; Becker, B.: Einfluss der Stichprobengröße auf die Bewertung der Überlebenswahrscheinlichkeit von Druckgefäßen aus Verbundwerkstoffen. TS 4 (2014) Nr. 7/8, S. 59-65.
[5] Becker, B.; Mair, G. W.: Risiko und Sicherheitsniveau von Composite-Druckgefäßen. TS 5 (2015) Nr. 11/12, S. 38-44
[6] Mair, G. W.: Sicherheitsbewertung von Composite-Druckgasbehältern – Potential statistischer Methoden jenseits aktueller Vorschriften, Berlin: Springer-Verlag 2016.
[7] Mair, G.W.: Safety Assessment of Composite Cylinders for Gas Storage by Statistical Methods – Potential for Design Optimisation Beyond Limits of Current Regulations and Standards, Springer International Publishing AG 2017
[8] Becker, B.; Mair, G. W.: Statistical analysis of burst requirements from regulations for composite cylinders in hydrogen transport. Materials Testing 59 (2017) 3, S. 226-232
[9] Mair; G. W., et al.:Composite storage systems for compressed hydrogen – systematic improvement of regulations for more attractive storage units, International Journal of Hydrogen Energy (2018), https://doi.org/10.1016/j.ijhydene.2018.04.068.
[10] Mair; G. W., et al.: Monte-Carlo-analysis of minimum load cycle requirements for composite cylinders for hydrogen, International Journal of Hydrogen Energy (2018), https://doi.org/10.1016/j.ijhydene.2018.09.185.
[11] DIN ISO 5479, Statistische Auswertung von Daten – Tests auf Abweichung von der Normalverteilung.
[12] EN 12245 (2012) Transportable gas cylinders – fully wrapped composite cylinders. CEN: European Standard, Brussels.
Dipl.-Ing.(FH) Manfred Spode, Arbeitsbereich „Themenfeld Energie – Gase“, Abt. 3 „Gefahrgutumschließungen“, Bundesanstalt für Materialforschung und prüfung (BAM); Berlin.
Dr.-Ing. Georg W.Mair Leitung Arbeitsbereich „Themenfeld Energie – Gase“, Abt. 3 „Gefahrgutumschließungen“, Bundesanstalt für Materialforschung und prüfung (BAM); Berlin.