Dämpfungsschlitze in Kreissägeblättern
In Kreissägeblättern werden Dehnungs- und Dämpfungsschlitze zur Verminderung von Schwingungen und zum Ausgleich thermischer Dehnungen genutzt. Mithilfe der Finite-Elemente-Methode (FEM) wurden Kreisscheiben mit einfachen Schlitzkonfigurationen analysiert, um Wirkmechanismen und Optimierungsmöglichkeiten zu identifizieren.

Bild 1. Geschlitzte Kreissägeblätter unterschiedlicher Anbieter: Leitz, Edessö Tools and More, Robert Bosch sowie Stehle/Ledermann (von links nach rechts). Bild: IfW
Die Wirkungsweise der Schlitze auf die dynamischen Eigenschaften besteht einerseits in der Dämpfungswirkung, andererseits in der Modifikation der Schwingungseigenformen. Mithilfe der FEM-Analyse sollen Zusammenhänge einzelner Schlitzparameter mit den statischen und dynamischen Eigenschaften von Kreissägeblättern ermittelt werden. Zur Validierung des entwickelten Simulationsmodells dienen analytische Berechnungen.
Kreissägeblätter sind aus der heutigen Produktionswelt nicht mehr wegzudenken. Im Vergleich zu anderen Trennverfahren bietet das Kreissägen Vorteile sowohl in der erzielten Qualität der Schnitte – bemessen an der Oberflächenrauheit der Schnittflächen – als auch in wirtschaftlichen Kriterien wie den erreichbaren Schnittraten oder den Schnittkosten [1]. Kreissägen kommen sowohl bei der Fertigung von hohen Stückzahlen mit hohem Automatisierungsgrad, aber auch bei der handwerklichen Fertigung von Einzelstücken und Kleinserien zum Einsatz.
Ausgangssituation
Die dynamischen und statischen Eigenschaften der Kreissägeblätter üben großen Einfluss auf die Schnittqualität des bearbeiteten Werkstücks aus. Insbesondere in der Holzbearbeitung mit hohen Drehzahlen spielen diese Merkmale eine bedeutende Rolle [2]. Bedingt durch ihre geometrische Form und die Einsatzart sind Kreissägeblätter schwingungsanfällig. Korreliert die Drehfrequenz mit einer Eigenfrequenz des Kreissägeblatts, können große axiale Schwingungsamplituden auftreten und die Prozessstabilität verschlechtern [3]. Der Zerspanprozess sowie die auftretende Reibung zwischen dem Sägeblatt und dem Werkstück trägt Wärmeenergie in das Werkzeug ein, was zu Wärmespannungen und -dehnungen führen kann. Beide Effekte beeinflussen sowohl die Standzeit des Werkzeugs als auch die Oberflächenqualität des Werkstückes negativ.
Um diese instabilen Prozessbedingungen zu vermeiden, werden als passive Maßnahme Schlitze in den Werkzeug-Grundkörper (Stammblatt) eingebracht. Zunächst wurden lediglich Dehnungschlitze am äußeren Rand des Werkzeugs verwendet. Diese nehmen die durch den Sägeprozess verursachte Wärmedehnung am Umfang auf. Sie verhindern dadurch, dass das Sägeblatt in den Randbereichen Wellen wirft und insgesamt in eine Richtung ausbeult [4].
Später kamen Dämpfungsschlitze im Inneren des Stammblattes hinzu. Damit können die Eigenfrequenzen des Sägeblatts beeinflusst und das Dämpfungsverhalten verbessert werden. Die Schwächung des Stammblatts bewirkt eine Relativbewegung der Blattsegmente, wodurch eine höhere Energiedissipation erreicht werden kann. Zudem behindern die Schlitze die Ausbreitung der Eigenschwingungen auf dem Sägeblatt. Eingebrachte Schlitze bringen vor allem bei kleinen Zahnvorschüben merkliche Verbesserungen mit sich, bei großen Zahnvorschüben können sie sich hingegen negativ auswirken: Dem Werkzeug werden durch die Einwirkung der Passivkräfte Schwingungen aufgezwungen, die nicht den Eigenfrequenzen entsprechen. Es kommt hier vielmehr zu einer Verbiegung der Blattsegmente gegeneinander [5;6].
Bisher sind die Zusammenhänge zwischen Formgebung und Wirksamkeit der Schlitze kaum geklärt; nur einzelne vordefinierte Schlitzkonfigurationen wurden näher untersucht [7;8]. Deshalb sind die verwendeten Schlitzformen in der Praxis sehr vielfältig, Bild 1, und auch Gegenstand zahlreicher Patentdokumente. Die Entwicklung der Schlitzkonfigurationen wird oftmals lediglich unter Anwendung empirischer Erfahrungswerte durchgeführt.
Um Dämpfungs- und Dehnungsschlitze künftig optimal auslegen und Konstruktionsempfehlungen geben zu können, wird mithilfe der FEM ein Modell erstellt, dessen Ergebnisse nachfolgend dargestellt werden. Mit diesem Simulationsmodell ist es möglich, sowohl vorbestimmte Schlitzgeometrien zu bewerten als auch Parameterstudien der gesamten Schlitzkonfiguration durchzuführen. Zur Validierung des Modells dienen die Eigenfrequenzen und -formen einer ungeschlitzten Kreisscheibe, die mit einer analytischen Lösung verglichen werden [9]. Zusätzlich zu den dynamischen Eigenschaften wird zur Bewertung die statische Steifigkeit der Sägeblätter herangezogen.
Simulationsmodell
Zur Definition der Randbedingungen für die FE-Simulation und Modellkalibrierung dienen analytische Berechnungen. Die Kalibrierung wird an einer stillstehenden Kreisscheibe mit einem Außendurchmesser von 350 mm, einer Mittelbohrung von 30 mm und 2,5 mm Dicke durchgeführt. Dieses Evaluationsmodell hat zunächst keine Schlitze. Tabelle 1 gibt die Werkstoffparameter an, die den in dieser Arbeit ermittelten Simulationsergebnissen zugrunde liegen. Die gelisteten Werte entsprechen realen Werkstoffkennwerten für den Kreissägeblattstahl 75Cr1.
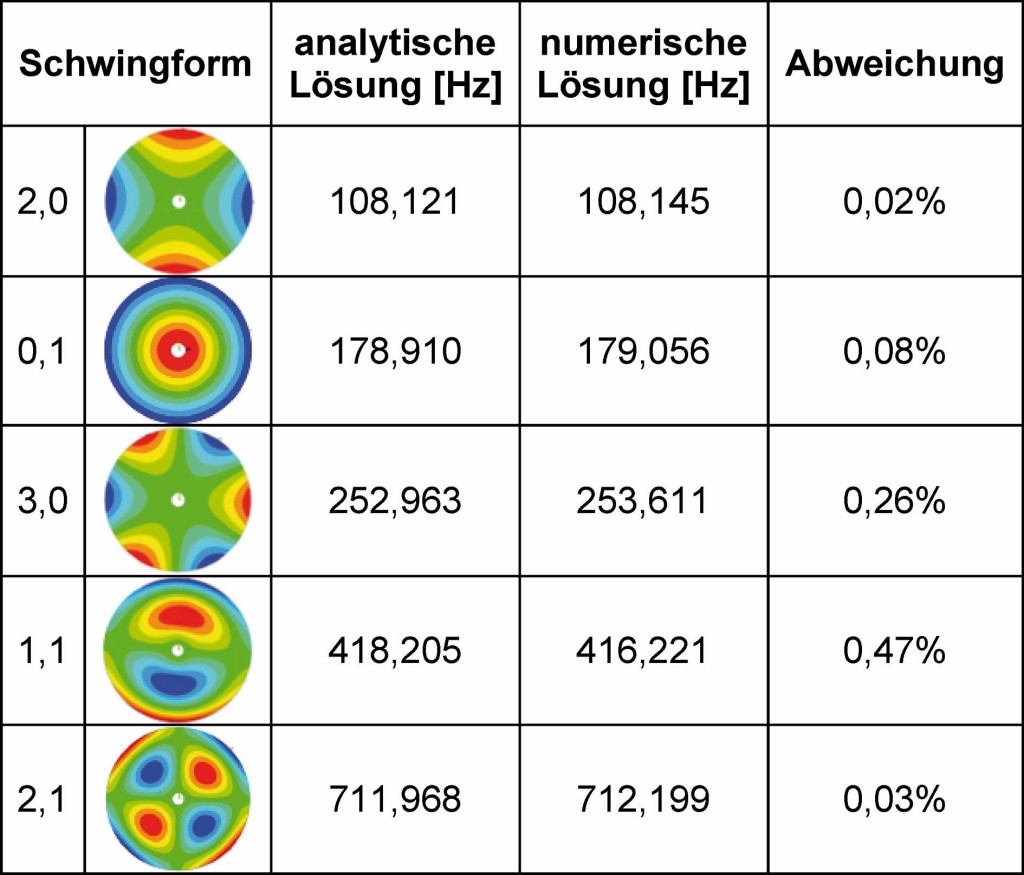
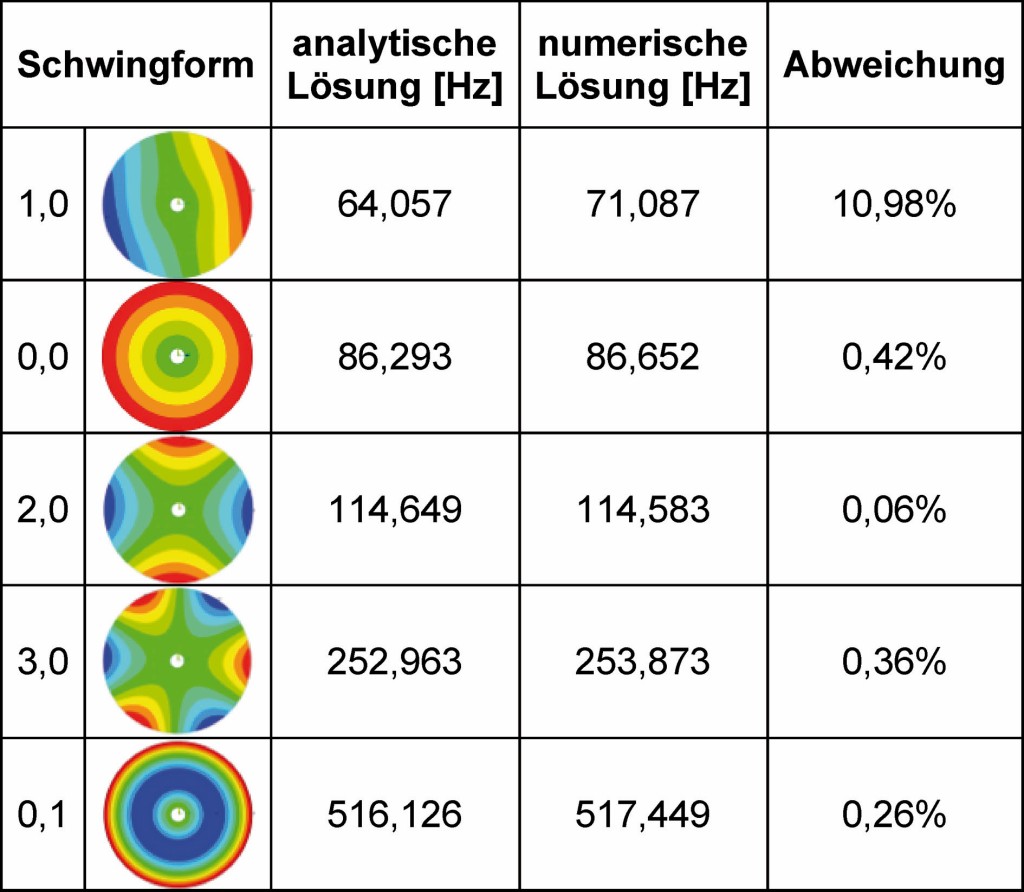
Der Abgleich wurde sowohl für eine mittig über einen Flansch eingespannte Kreisscheibe (DFlansch = 50 mm) als auch für eine frei schwingende Scheibe ohne weitere Randbedingungen durchgeführt. Eine Gegenüberstellung der analytischen und numerischen Lösungen ist in Tabelle 2 und Tabelle 3 wiedergegeben. Sie zeigen eine sehr gute Übereinstimmung für die relevanten Moden. Die Bezeichnung der Schwingungsformen setzt sich bei Kreisscheiben aus der Anzahl ihrer Knotendurchmesser und ihrer Knotenkreise zusammen.
Um das Simulationsmodell effizient für die Berechnung verschiedener Schlitzgeometrien und -anordnungen zu verwenden, sollte dieses eine einfache Anpassung der Schlitze inklusive ihrer Parametrisierung zulassen. Die Vernetzung, Berechnung und Auswertung sollte automatisiert durchführbar sein. Hierzu wurde eine Kombination aus CAD-System und FEM-Software genutzt.
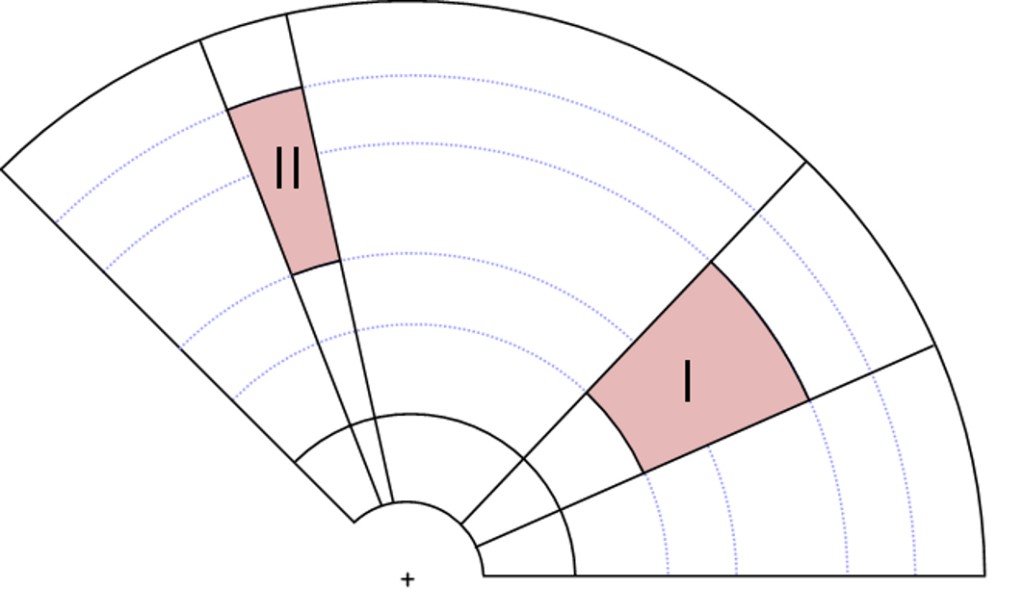
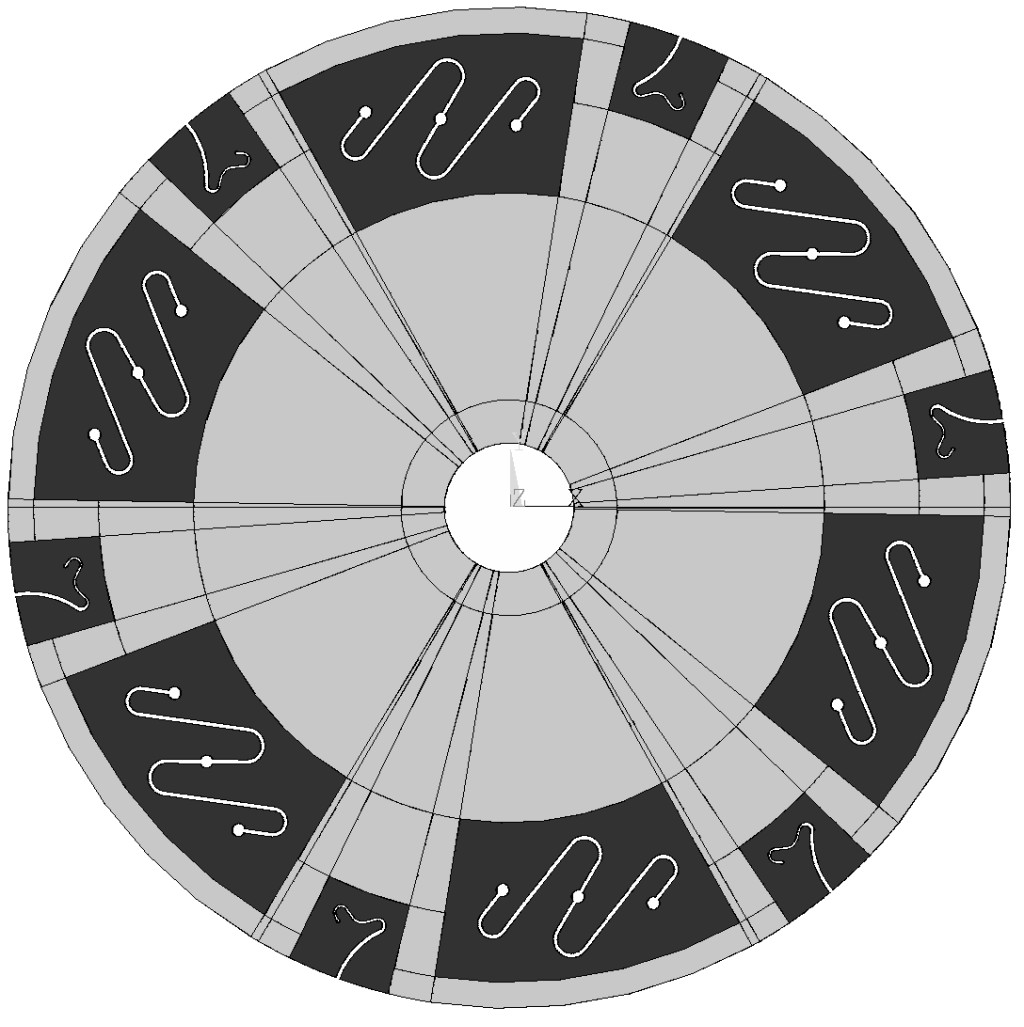
Zentrales Element der parametrischen automatisierten Modellierung ist die Aufbereitung der Geometrie und die Vernetzung. Grundgedanke der Umsetzung ist, das Gesamtmodell zu zerlegen und in Einzelteilen zu modellieren, die einfacher zu handhaben sind. Im ersten Schritt wird das Gesamtmodell unter Voraussetzung der Rotationssymmetrie auf ein Einzelsegment reduziert. Dieses Segment lässt sich wiederum aufteilen in Bestandteile mit unregelmäßigen Geometrien und in einfache Kreisringsegmente. Diese Zerlegung ist in Bild 2 (links) schematisch dargestellt: Die Teilstücke I und II enthalten die Schlitze und sind im Gesamtsegment frei positionierbar. Rechts davon ist als Beispiel eine rekonstruierte Gesamtgeometrie zu sehen.
Dieser vorgestellte zweite Unterteilungsschritt erlaubt es, für jeden Bereich die am besten geeignete Vernetzungsmethode zu wählen: Unstrukturierte Netze für die komplexen Geometriebereiche mit Schlitzen erlauben eine genaue Abbildung der Schlitze, während die strukturierte Vernetzung der übrigen Bereiche die Genauigkeit des Gesamtmodells erhöht und die benötigte Rechenzeit der FE-Simulation deutlich reduziert. Eine hierfür programmierte Schnittstelle zwischen CAD und FE-System übernimmt die automatische Vernetzungssteuerung sowie das weitere Pre-Processing und die Übergabe an den Solver.
Parameterstudie
Repräsentativ für die Vielfalt der Schlitzkonfigurationen wird eine Parameterstudie zu einfachen, geraden Schlitzgeometrien vorgestellt. Hierbei wird jeweils ein Parameter variiert, während die anderen mit realitätsnahen Werten initialisiert und konstant gehalten werden. Als Referenz für die Beurteilung wird die ungeschlitzte Kreisscheibe der Validierungsrechnung verwendet. Diese Abmaße werden auch in den weiteren Simulationsrechnungen verwendet. Der Außendurchmesser der Scheibe beträgt Da = 350 mm, der Bohrungsdurchmesser Db = 3 mm und die Dicke h = 2,5 mm.
Bei der statischen Analyse ist die Scheibe bis zu einem Einspanndurchmesser von DFlansch = 50 mm fixiert, während die Modalanalyse an einer frei schwingenden Scheibe simuliert wird. Als Kennwerte zum Vergleich dienen die Eigenfrequenzen der Kreisscheibe und die statische Steifigkeit. Unter der statischen Steifigkeit cst einer durch eine Einzellast am Rand belasteten Kreisscheibe versteht man das Verhältnis von aufgebrachter Einzellast F zu der Durchbiegung w unter dieser Einzellast [3].
Zunächst wird der Einfluss der Länge von radial ausgerichteten Außenschlitzen betrachtet; die simulierte Scheibe hat keine Innenschlitze. Die Anzahl der Schlitze wird bei dieser Rechnung mit na = 6 konstant gehalten und die Schlitzbreite auf ba = 1,5 mm festgesetzt, Tabelle 4.
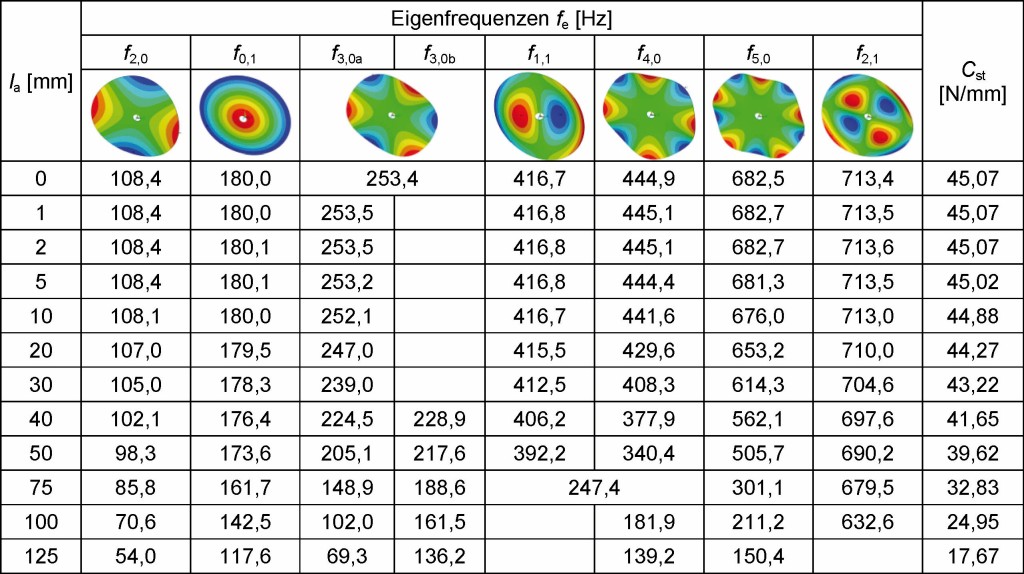
Tabelle 4. Eigenfrequenzen und Steifigkeit der Kreisscheibe in Abhängigkeit von der Schlitzlänge. Bild: IfW
Mit zunehmender Strukturschwächung sinken sowohl die Eigenfrequenzen als auch die statische Steifigkeit. Bemerkenswert ist dabei die Rate, mit der dies passiert. Moden mit Knotenkreisen reagieren weitaus weniger empfindlich auf Vergrößerungen der Schlitzlänge als solche ohne.
Mit fortschreitender Schlitzlänge bilden sich zwei Varianten zu Eigenformen mit Knotendurchmessern aus: eine davon mit den Maximalamplituden an den Schlitzen, die andere mit Knotendurchmessern an den Schlitzen, Bild 4.
Bei der Mehrzahl dieser Schwingungsformen ist eine zugehörige Aufteilung der Eigenfrequenzen kaum bemerkbar oder kleiner als die Ungenauigkeit der Simulationsrechnung. Wie in Tabelle 4 an den Eigenfrequenzen der Schwingform mit drei Knotendurchmessern (f3,0a und f3,0b) zu sehen ist, kann der Frequenzunterschied bei den Schwingformen, deren Knotendurchmesser mit der Schlitzanzahl oder deren Vielfachen übereinstimmen, jedoch sehr groß werden.
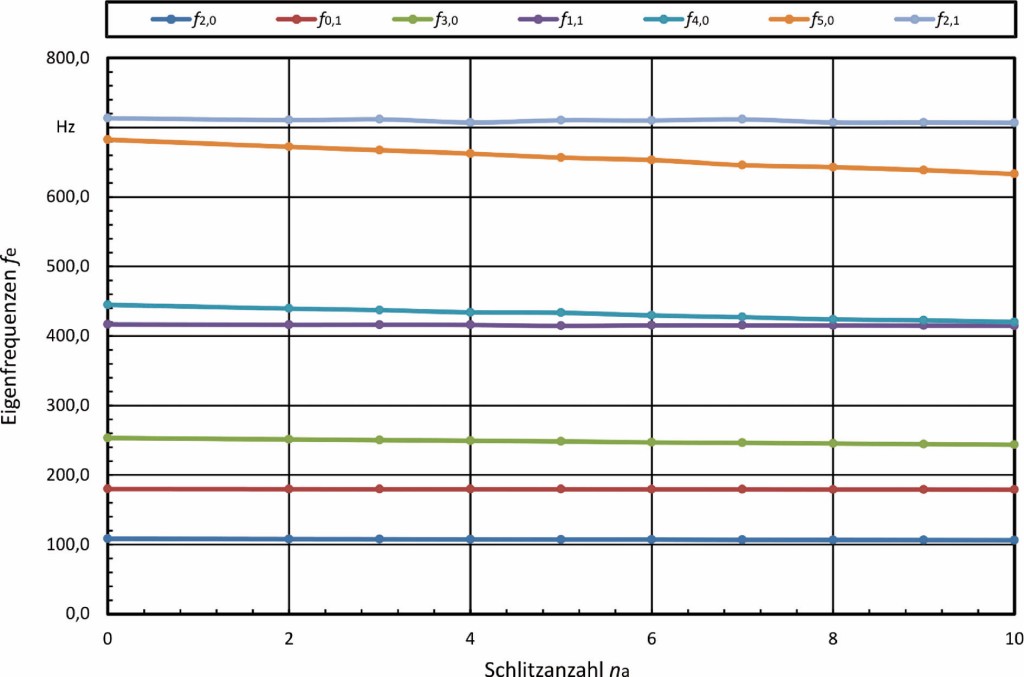
Wird nur die Anzahl der Schlitze verändert (na = 0 … 10) bei sonst gleichbleibenden Parametern und einer konstant gehaltenen Schlitzlänge, deren Größenordnung der realer Kreissägeblätter entspricht (la = 20 mm), zeigt sich, dass mit zunehmender Anzahl die Steifigkeit und auch die Eigenfrequenzen sinken. Bei den meisten Schwingformen ist dies weit weniger ausgeprägt als bei der Variation der Schlitzlänge. Deutlich zu erkennen ist diese Tendenz in diesem Fall nur bei den Eigenfrequenzen der (4,0)- und der (5,0)-Mode, Bild 5.
Die Variation der Breite von Außenschlitzen von ba = 0,1 … 5 mm (bei sonst konstanten Schlitzparametern) hat praktisch keinen Einfluss auf die Eigenfrequenzen und die statische Steifigkeit. Eine Modifikation der dynamischen Charakteristik über die Schlitzbreite als Parameter erscheint damit nicht zielführend.
Studien zur radialen und tangentialen Ausdehnung von geraden Innenschlitzen sowie deren Anzahl kommen zu einem vergleichbaren Ergebnis wie bei Außenschlitzen, jedoch mit schwächerem Einfluss auf Eigenfrequenzen und statische Steifigkeit.
Zusammenfassung und Ausblick
Unabhängig von Anzahl, Position und Form beeinflusst jede der untersuchten einfachen Schlitzvarianten Eigenschaften der Kreisscheibe negativ: Die Eigenfrequenzen fast aller Schwingformen werden reduziert; ebenso sinkt die statische Steifigkeit mit jeder Verletzung der Struktur. Einen großen Einfluss scheint dabei die Ausrichtung der Unterbrechungen zu haben. Radiale Schlitze beeinflussen die Eigenschaften viel deutlicher als tangential angeordnete. Jede Form von eingebrachten Schlitzen zieht eine Aufspaltung der Moden mit Knotendurchmessern nach sich. Die Ausprägung dieser Teilung ist stark abhängig von der Anordnung und Anzahl der Schlitze. „Passen“ die Schwingformen dabei in das Schlitzschema, liegen die Eigenfrequenzen der aufgespaltenen Mode weiter auseinander als bei schlechter Übereinstimmung. Die niedrigere der beiden Eigenfrequenzen wird dabei im Vergleich zur ungeschlitzten Scheibe besonders deutlich verringert.
Ursächlich für die im Bearbeitungsprozess störenden Eigenfrequenzen sind in aller Regel die Moden mit 0, 2, 3 Knotendurchmessern sowie keinem oder einem Knotenkreis. Wenn ausschließlich auf die untersuchten Zielgrößen (Eigenfrequenzcharakteristik und Steifigkeit) hin konstruiert und optimiert wird, sollte die Anzahl der einzubringenden Schlitze möglichst kein ganzzahliges Vielfaches von zwei oder drei sein. Dehnungsschlitze am äußeren Rand beeinflussen die Eigenschaften besonders und sollten möglichst klein gestaltet werden.
Das vorliegende Simulationsmodell erfasst bisher nur die Eigenfrequenzen von stillstehenden Kreisscheiben und deren statische Steifigkeit im eingespannten Zustand. Für detaillierte Konstruktionsempfehlungen für Kreissägeblätter bedarf es einer Erweiterung des Modells. Im nächsten Schritt wird daher das Modell um die Rotation des Werkzeugs ergänzt, sodass statt einer Näherung über die Eigenfrequenzen kritische Drehzahlen und Betriebsbedingungen im Eingriff beurteilt werden können. Auch muss es künftig möglich sein, sowohl die Dämpfung im Betriebspunkt als auch von mit viskoelastischen Materialien gefüllten Dämpfungsschlitzen zu bewerten.
Nach einer Erstveröffentlichung in der wt Werkstattstechnik online 105 (2015), Nr. 1/2, S. 41–46 (www.werkstattstechnik.de).
Der Weiterentwicklung des Simulationsmodells widmet sich das von der Deutschen Forschungsgemeinschaft (DFG) geförderte Forschungsprojekt HE 1656/162–1 „Schwingungen von Kreissägeblättern, Berechnung mit FE-Modellen, Pfadverfolgung, Eigenwerte, Stabilität, experimentelle und numerische Modalanalyse“. Die daran beteiligten Mitarbeiter sind eingebunden in das Stuttgarter Kompetenzzentrum Sägen.
Literatur:
Münz, U.V.: Trennen durch Kreissägen. Industrieanzeiger 114 (1992), Nr. 16, S. 46–48. Heisel, U.; Mishev, A.: Verbesserte Kantenqualität beim Kreissägen in Bearbeitungszentren – Entwicklung eines Kreissägeaggregates mit integrierter Schrägstelleinrichtung für CNC-Bearbeitungszentren. HOB (2010), Nr. 10, S. 66–68.
Friebe, E.: Steifigkeit und Schwingungsverhalten von Kreissägeblättern für die Holzbearbeitung. Dissertation, Universität Braunschweig, 1973.
Barz, E.: Vergleichende Untersuchungen über das Spannen von Kreissägeblättern mit Maschinen und mit Richthämmern. Holz als Roh- und Werkstoff 21 (1963), Nr. 4, S. 135–144.
Rowinski, B.: Schwingungsverhalten und Schwingungsursachen von Kreissägeblättern. Dissertation, Universität Braunschweig, 1967.
Birenbaum, C.: Beitrag zur rechnerischen und experimentellen Auslegung von Kreissäge-Stammblättern für die Holzbearbeitung. Dissertation, Universität Stuttgart, 2013.
Nishio, S.; Marui, E.: Effects of Slots on the Lateral Vibration of a Circular Saw Blade. International Journal of Machine Tools and Manufacture 36 (1996), No. 7, pp. 771–787.
Yu, R.-C.; Mote, C. D.: Vibration of circular saws containing slots. Holz als Roh- und Werkstoff 45 (1987), Nr. 4, S. 155–160.
Blevins, R. D.: Formulas for natural frequency and mode shape. New York/USA: Van Nostrand Reinhold, 1979.
Prof. Dr.-Ing. Prof. h.c. mult. Dr. h.c. mult. Uwe Heisel, Jahrgang 1945, ist Ordinarius und Direktor des Instituts für Werkzeugmaschinen (IfW) der Universität Stuttgart. // Dipl.-Ing. Simon Weiland, Jahrgang 1982, ist akademischer Mitarbeiter am IfW. // Dr.-Ing. Christoph Birenbaum, Jahrgang 1981, ist Gruppenleiter am Fraunhofer-Institut für Produktionstechnik und Automatisierung IPA in Stuttgart.