Statistische Versuchsplanung – Methode zur Optimierung von Herstellungsverfahren
Wenn ein technisches System nicht die gewünschten Ergebnisse liefert, zum Beispiel bezüglich Ausschuss, Qualität, Anlageneffizienz oder Prozessleistung, ist es zur Problemlösung entscheidend, den Produktionsablauf zu verstehen – nur dann lassen sich erfolgreich Optimierungen finden.

Bild 1. Bei einem statistischen Versuchsplan zur Optimierung von Produktionsprozessen ist eine systematische Vorgehensweise unerlässlich. Bild: Hochschule Koblenz
Das gelingt häufig mithilfe der Erfahrung bereits länger beschäftigter Mitarbeiter und den vielen, jahrelang gewonnenen Erkenntnissen über die Prozessabläufe. Zudem kann die statistische Versuchsplanung helfen, Herstellungsverfahren zu verbessern.
Reicht bisher gesammeltes Wissen nicht aus, müssen neue Erkenntnisse gewonnen werden. Häufig versuchen Verantwortliche dann, aus früher generierten Informationen („Historische Daten“) oder mithilfe einer einfachen Prozessbeobachtung die Produktionsabläufe zu optimieren. Jedoch gibt es bei dieser Vorgehensweise einige Nachteile. Oft ist beispielsweise die Qualität historischer Daten unbekannt oder potentiell eher schlecht. Die Daten sind unvollständig oder passen nicht 100%ig zur Aufgabenstellung, sowohl Einflussgrößen im Prozess (x) als auch Outputmesswerte (y) können fehlen. Möglicherweise sind wichtige Variablen während des Zeitraums der Datenerfassung konstant geblieben und schließlich könnten durch eine unbewusste Korrelierung von Prozessvariablen falsche Eindrücke bezüglich der Auswirkungen dieser Variablen auf den gesamten Prozess entstehen.
Typische Fehler bei Versuchsläufen
Die Alternative ist dann, mithilfe von Versuchsläufen neue Informationen zu generieren, die bei der Problemlösung helfen. Dabei ist jedoch Vorsicht geboten. Wird hierbei nicht systematisch vorgegangen, können sich die Beteiligten schnell in den Wirrungen der Prozessparameter verlieren und es wird viel Zeit und Geld verschwendet, Bild 1. Beispielhaft sind nachfolgend drei typische Fehler genannt:
– Es wird nur jeweils ein Einflussfaktor verändert und nach dem Versuch zurückgesetzt: Problematisch bei diesem Vorgehen ist, dass Wechselwirkungen völlig unberücksichtigt bleiben. Das einfache Beispiel einer Wechselwirkung ist etwa, dass Vorschub und Schneidgeschwindigkeit bei einer Drehmaschine nicht losgelöst voneinander betrachtet werden können.
– Wenn ein Faktor Erfolg zeigt, wird diese Einstellung beibehalten: Auch hier bleiben Wechselwirkungen unberücksichtigt. Gefundene Optima sind gegebenenfalls nur lokale Optima.
– Viele Faktoren werden auf einmal verändert: Entscheidender Nachteil dieser Vorgehensweise ist, dass am Ende nicht klar ist, welcher Faktor tatsächlich welchen Beitrag zu einem potentiellen Optimierungserfolg geleistet hat.
Statistische Versuchsplanung liefert aussagekräftige Daten
Mit der statistischen Versuchsplanung (Design of Experiment, DoE) wurde eine Methode entwickelt, um diesen Problemen vorzubeugen und aussagekräftige Daten passend zur Aufgabenstellung zu generieren. Ein einfach nachvollziehbares Bespiel ist der Siegelprozess beim Verschließen eines Joghurtbechers aus Kunststoff. Vereinfacht lässt sich darstellen: Die benötigte Kraft, um den Becher zu öffnen („y“), ist abhängig vom Druck beim Siegeln (x1), von der Siegeltemperatur (x2) und der Siegelzeit (x3). Ziel der Versuche ist, den Zusammenhang zwischen dem y „Aufreißkraft“ und den Einflussgrößen (x) zu verstehen sowie mathematisch zu beschreiben. Wird nun für jede der Einflussgrößen je ein niedriger Wert und ein hoher Wert als mögliche Einstellung festgelegt, ergeben sich acht verschiedene Prozesseinstellungen, Tabelle.
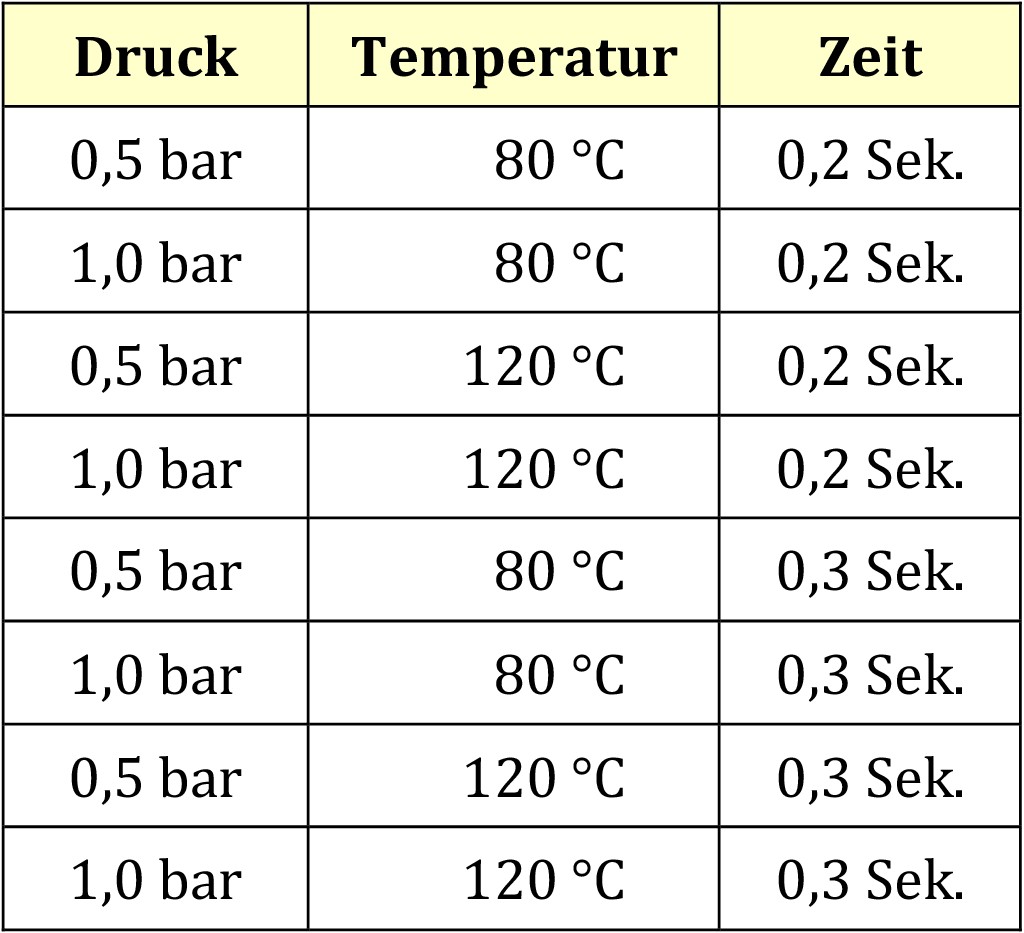
Tabelle. Werden für drei Einflussgrößen je ein hoher und ein niedriger Wert festgelegt, ergeben sich bereits acht verschiedene Prozesseinstellungen. Bild: Hochschule Koblenz
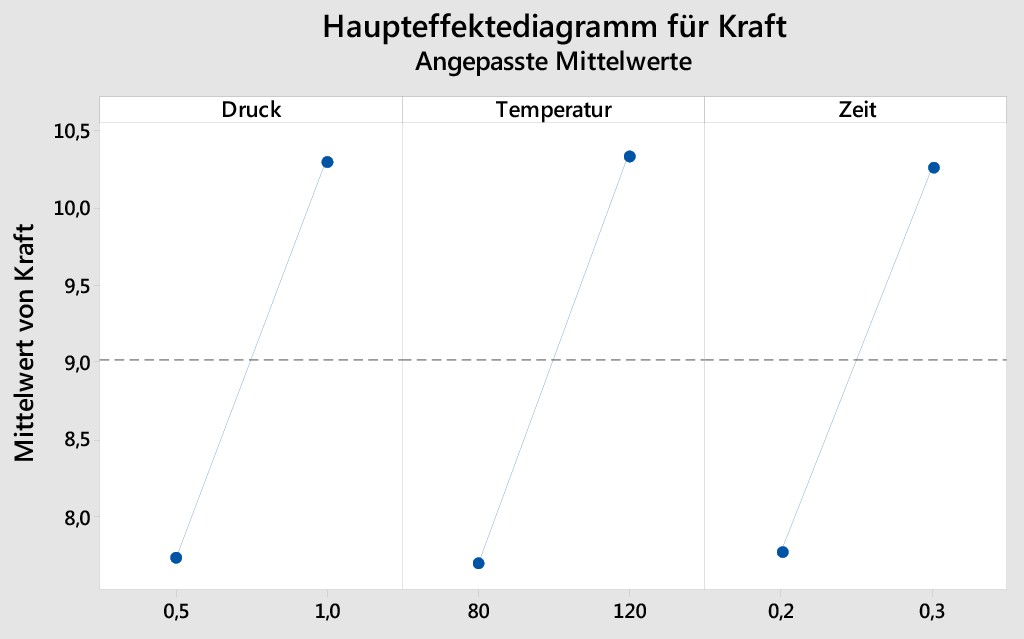
Bild 2. Exemplarische Darstellung, wie die drei Prozessparameter Druck, Temperatur und Zeit die Ergebnismessgröße „Aufreißkraft“ beeinflussen. Bild: Hochschule Koblenz
Dieses Szenario ist ein systematischer Versuchsaufbau und wird in der Praxis als statistischer Versuchsplan bezeichnet. Mithilfe der Varianzanalyse kann dieser Plan nach Durchführung der Versuche ausgewertet werden. Es ergibt sich eine Darstellung wie beispielsweise in Bild 2: Hier zeigen sich die Einflüsse der drei Prozessparameter Druck, Temperatur und Zeit auf die Ergebnismessgröße „Aufreißkraft“.
In ähnlicher Art können auch Wechselwirkungen visualisiert werden. Der Zusammenhang ist darüber hinaus mit einer Gleichung mathematisch beschreibbar, hier exemplarisch:
Aufreißkraft = -7,7 + 5,2 Druck
+ 0,066 Temperatur
+ 25 Zeit
9-Punkte-Fahrplan für die Praxis
Die genannten Beispiele klingen plausibel und einfach umsetzbar. In der Praxis gibt es jedoch zahlreiche „Stolperfallen“, denn auch bei DoE gilt, dass jedes statistische Hilfsmittel in der Ergebnisqualität nur so gut sein kann, wie die den Berechnungen zugrunde liegende Datenqualität. Daher gilt es für eine gelungene Prozessanalyse mithilfe eines statistischen Versuchsplans einige Faktoren zu beachten. Der folgende „9-Punkte-Fahrplan“ kann praktische Unterstützung liefern.
1. „Bestimmen der Ergebnisgrößen“: Die Ergebnismessgrößen müssen mit ausreichender Genauigkeit und Präzision messbar sein. Je höher das Rauschen in den gemessenen Daten, umso geringer die Chance, in der Auswertung der Versuche signifikante Einflussfaktoren zu finden. Daher ist es anzuraten, die Messmittelfähigkeit vor der Durchführung eines statistischen Versuchsplans sicherzustellen, Bild 3.

Bild 3. Es ist dringend anzuraten, die Messmittelfähigkeit vor der Durchführung eines statistischen Versuchsplans sicherzustellen. Bild: Hochschule Koblenz
Es muss geklärt sein, wie es um die Genauigkeit, die Wiederholbarkeit, die Reproduzierbarkeit und die Auflösung des Messsystems bestellt ist. Zu empfehlen ist, eine Messsystemanalyse durchzuführen.
2. „Bestimmung der zu untersuchenden Faktoren und der Faktorausführungen“: Die Festlegung der zu untersuchenden Faktoren sollte sorgfältig geprüft und dazu ein Team von Fachleuten eingebunden sein. Wenn wichtige Einflussgrößen keine Berücksichtigung finden, sind die Ergebnisse unbefriedigend, vielleicht sogar nutzlos.
3. Sorgfältig sollte auch beim „Festlegen der Faktorausführungen“ (hoch / tief) vorgegangen werden. Nicht selten wird beim vorletzten Versuchslauf festgestellt, dass die Faktorausführungen so gewählt wurden, dass eine bestimmte Kombination im Produktionsprozess nicht lauffähig ist. Die Frage, ob alle Faktorausführungen miteinander kombinierbar sind, muss vor dem Experiment geklärt sein. Dann lassen sich gegebenenfalls Strategien definieren, wie diese Kombinationen zu vermeiden sind – oder es müssen andere, weniger kritische Ausführungen gewählt werden. Wichtig ist auch, dass die Faktorausführungen reproduzierbar sind. Es gilt also sicherzustellen, dass eine Faktorausführung, die erneut eingestellt wird, genau den Werten der ersten Einstellung entspricht. Jede Unsicherheit beim Reproduzieren der Faktoreinstellungen führt zu einem weiteren Verrauschen der Messergebnisse.
4. Bei der „Auswahl des Designs“ ist zu beachten, dass auch bei der statistischen Versuchsplanung die Stichprobengröße die Trennschärfe bei der Auswertung maßgeblich mit beeinflusst. Es sollten Berechnungen zum erforderlichen Stichprobenumfang – und damit zur Anzahl der Replikationen der Versuchsläufe – durchgeführt werden. Ein positiver Nebeneffekt ist, dass diese Berechnungen auch dazu „zwingen“, über die Größe eines relevanten Effekts nachzudenken, der sich detektieren lässt. Das sorgt zusätzlich für mehr Sicherheit.
5. Beim „Erstellen des Versuchsplans“ ist auf die Randomisierung der Versuchsläufe zu achten, um valide Aussagen zu den Einflüssen einzelner Faktoren zu bekommen. Wenn es Faktoren gibt, deren Einstellungen nur schwer veränderbar sind, empfiehlt sich ein „Split-Plot-Design“. In diesem Fall werden die schwer veränderbaren Faktoren nicht so oft verstellt und diese Besonderheit bei der Berechnung der Ergebnisse berücksichtigt.
6. Bei der „Durchführung der Experimente“ ist es wichtig, die Durchführenden für die Notwendigkeit einer sorgfältigen Arbeitsweise, einer möglichst großen Präzision bei der Einstellung der Faktorstufen sowie einer strikten Einhaltung der Versuchsreihenfolge und der Dokumentation aller besonderen Vorkommnisse zu sensibilisieren.
7. Bei der „Datenanalyse“ sollte bedacht werden, dass die Nullhypothese nie bewiesen wird: Nur weil ein Faktor nicht signifikant erscheint, bedeutet es nicht, dass er keinen Einfluss hat. Vielleicht war die Stichprobengröße nur zu gering? Auch Wechselwirkungen können einzelne Faktoren nicht signifikant erscheinen lassen.
8. „Gegebenenfalls weitere DoE durchführen“: Nur selten ist nach einem einzigen DoE schon „alles klar“ und der Prozess vollumfänglich verstanden. In aller Regel sind mehrere Durchläufe notwendig, um sich iterativ einem vollen Prozessverständnis zu nähern. Das sollte auch bei der Budgetplanung Berücksichtigung finden.
9. Die „abschließende Verifizierung der Ergebnisse“ sollte ein gefundenes Optimum bestätigen. Dazu sollten noch einmal Versuche mit den optimalen Einstellungen gemacht werden. Diese Bestätigungsläufe zur Verifizierung der Ergebnisse sind gut investiertes Geld.
www.hs-koblenz.de/profile/leyendeck
Prof. Dr. Bert Leyendecker ist Professor an der Hochschule Koblenz im Fachbereich Produktionswirtschaft und Projektmanagement.









