Kopfrechnen: Wie kann ich es verbessern?
Haben Sie sich auch schon einmal dabei ertappt, wie Sie die einfachsten Rechnungen in ihr Smartphone eingetippt haben? Schluss damit. Wir haben Trainingstipps für Sie gesammelt, damit es das nächste Mal mit dem Kopfrechnen klappt.

Foto: panthermedia.net/ok_kate
Direkt zu:
Tomohiro Iseda ist der schnellste Kopfrechner der Welt. Bei der WM 2018 in Wolfsburg musste der Japaner in Windeseile zehn zehnstellige Zahlen addieren, zwei achtstellige Zahlen multiplizieren und von sechsstelligen Zahlen die Wurzel berechnen. Für den modernen Menschen, dessen Smartphone bereits mit einem Taschenrechner ausgestattet ist, eine geradezu skurrile Vorstellung. Und dennoch: Zahlenverständnis und Datenkompetenz sind Skills, die wichtiger werden – gerade für Ingenieure und Informatiker. Außerdem bringt Kopfrechnen die grauen Zellen in Schwung. Aber wie wird man ein besserer Kopfrechner? Einfache Antwort: nur durch Üben, Üben, Üben. Ingenieur.de hat ein paar Trainingstipps für Sie gesammelt.
Der Berger-Trick
Auch Andreas Berger ist ein Ass im Kopfrechnen. Bei der letzten Weltmeisterschaft in Wolfsburg belegte der Thüringer Platz 17. Dabei mussten die Teilnehmer unter anderem diese drei Aufgaben lösen – so schnell wie möglich und ohne Hilfsmittel:
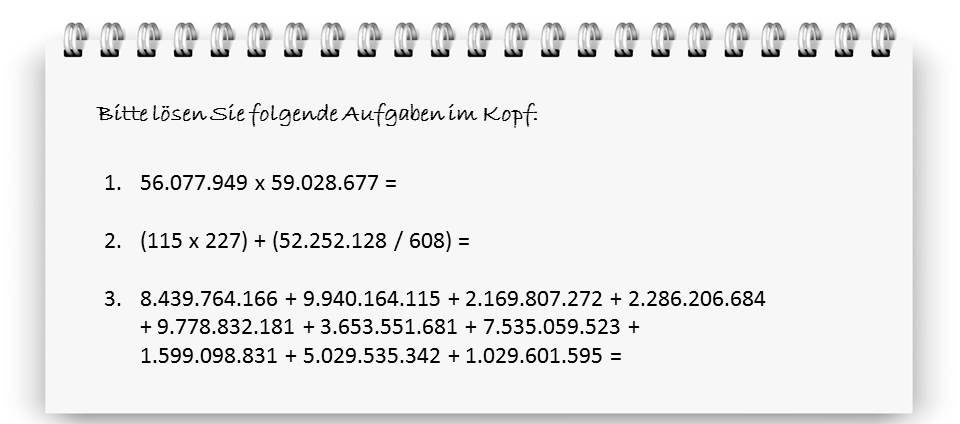
Das ist für Anfänger nicht zu machen. Berger empfiehlt, eine zweistellige Zahl, die eine 5 am Ende hat, mit sich selbst zu multiplizieren – zum Beispiel die 75. Das sei „etwas Kleines für den Anfang“, sagt er gegenüber ingenieur.de, dürfte einem ungeübten Rechner aber schon Schweißperlen auf die Stirn treiben. Berger nutzt dafür diesen Trick, der ursprünglich aus der Vedischen Mathematik kommt (dazu später noch mehr):
Der Akanji-Trick
Manuel Akanji sorgte Ende 2018 im Schweizer Fernsehen für Verwunderung. Der Verteidiger von Borussia Dortmund, zugleich Schweizer Nationalspieler, multiplizierte vor laufender Kamera 24 mit 75 – in weniger als drei Sekunden. 1.800 hieß die richtige Lösung. Wie hatte er das gemacht?
Vermutlich hat Akanji kreuzweise multipliziert. Mit etwas Übung können Sie auf diese Weise jede beliebige zweistellige Zahl mit einer anderen multiplizieren. Einen Zeitvorteil erreichen Sie wohlgemerkt nur, wenn Sie den Rechenweg so sehr verinnerlicht haben, dass Sie ihn automatisch durchführen. Das gelingt – wie schon erwähnt – nur durch ganz viel Übung. Einige Rechenbeispiel:
Der Trick mit dem Großen Einmaleins
Das kleine Einmaleins (1 x 1 bis 9 x 9) sollte sitzen. Das große Einmaleins (10 x 10 bis 19 x 19) ist weniger geläufig. Mit diesem Trick sparen Sie sich das Auswendiglernen. Wie rechnet man zum Beispiel 17 x 17 oder 19 x 18? Am einfachsten geht es so:
Die Trachtenberg-Methode
Jakow Trachtenberg war ein russischer Ingenieur, der eine Schnellrechenmethode entwickelte. Einem größeren Publikum bekannt wurde sie aber erst nach seinem Tod im Jahr 1953. Mit der Trachtenberg-Methode können Sie einstellige Zahlen leicht multiplizieren – ohne das kleine Einmaleins auswendig zu können. Es gibt aber einen Haken. Für jeden Multiplikator müssen Sie eine andere Rechenoperation anwenden. Wenn Sie sich an Ihren Schullehrer halten, müssten Sie bei der folgenden Rechnung jede Ziffer mit der 6 multiplizieren.
| 482 x 6 | |||
| 1 | 2 | ||
| 4 | 8 | ||
| 2 | 4 | ||
| 2. | 8 | 9 | 2 |
Mit der Trachtenberg-Methode geht es – etwas Training vorausgesetzt – einfacher. Dabei addieren Sie bei einstelligen Multiplikatoren jede Ziffer der ersten Zahl mit ihrem halben Nachbarn. Sie fangen rechts an. Auch für zweistellige Multiplikatoren hat Trachtenberg eigene Formeln entwickelt. Zum Beispiel für die 11. Dabei addieren Sie jede Ziffer der ersten Zahl einfach mit Ihrem Nachbarn. Zwei Rechenbeispiele:
Hinweis: In den Beispielen war das Ergebnis der einzelnen Rechenschritte nie größer als 10. Ist das der Fall, müssen Sie noch einen Übertrag von 1 oder maximal 2 mit einrechnen.
Der Inder-Trick
Die Inder haben im frühen 20. Jahrhundert die Vedische Mathematik hervorgebracht. Sie ähnelt der Trachtenberg-Methode, enthält aber noch zusätzliche Abkürzungen. Zum Beispiel können Sie sehr schnell subtrahieren, auch mit großen und ungeraden Zahlen. Und das Prinzip funktioninert auch beim Multiplizieren. Hier einige Beispiele:
Zum Schluss noch ein relativ einfaches Rechenbeispiel für Sie zum Üben:
| Übung zum Kopfrechnen mithilfe des Inder-Tricks | |
| Rechenaufgabe: | 91 x 91 |
| Beide Zahlen haben einen Abstand von 9 zur 100. Nun rechnen Sie: | 91 – 9 = 82 |
| Nächster Schritt: | 9 x 9 = 81 |
| Das zweite Ergebnis an das erste anhängen: | 8281 |
| Das Endergebnis lautet: | 91 x 91 = 8.281 |
So einfach kann Kopfrechnen sein.
Ein Beitrag von:




























