Rätsel Einstein-Kachel – auch physikalisch faszinierend
Die Einstein-Kachel war ein Rätsel, das einige Generationen an Mathematikerinnen und Mathematiker beschäftigte: Wie lässt sich aus lediglich einer Fliesenform ein Boden verlegen, dessen Muster sich niemals wiederholt? Im Jahr 2023 wurde der heilige Gral geknackt. Eine Forschungsgruppe aus Frankreich hat sich das Muster nun einmal aus physikalischer Sicht angeschaut.
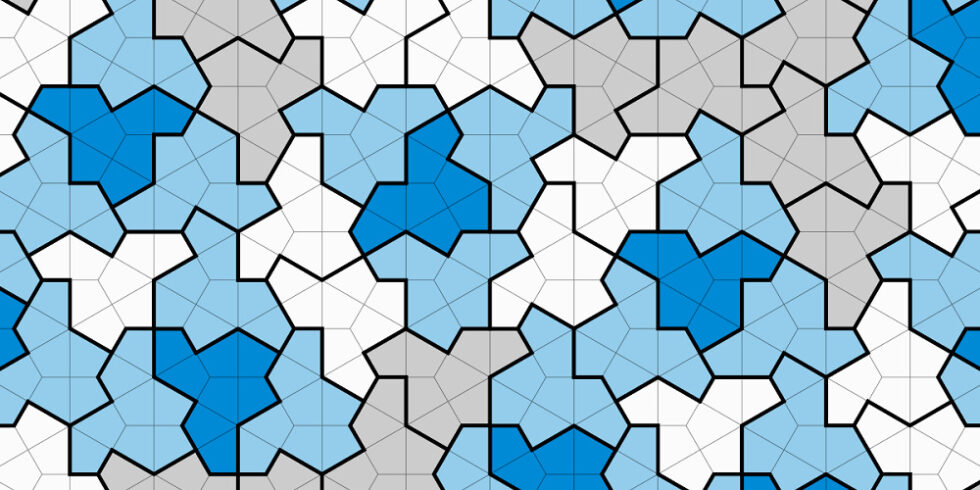
Mit der Einstein-Kachel lässt sich eine Ebene lückenlos bedecken, ohne dass sich das Muster jemals wiederholt.
Foto: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss / Einstein-Kachel / CC BY-SA 4.0 CC BY-SA (Ausschnitt)
Kreative Handwerkerinnen und Handwerker können Fliesenböden mit zahlreichen Mustern legen. Sie benötigen dafür jedoch in der Regel verschiedene Fliesenformen und trotzdem wiederholen sich irgendwann die Muster. Das hat die Mathewelt auf den Plan gerufen. Schon seit Jahren tüftelt sie an der einen Fliese, mit der sich unendlich viele Muster verlegen lassen, die sich niemals wiederholen. Nun scheint das Rätsel gelöst: Es gibt tatsächlich eine Einstein-Kachel, mit der das möglich ist. Und nicht nur das, ein Forscher hat nun den physikalischen Nutzen eines Kristallgitters erforscht, das dem Muster der Einstein-Kachel folgt.
Wie kam es zu der Einstein-Kachel?
Eins vorweg – die Einstein-Kachel hat keineswegs etwas mit dem genialen Physiker Albert zu tun, es geht vielmehr um den einen Stein (Fliese oder Kachel), mit dem sich die unendlich vielen Muster verlegen lassen. Nachdem sich Generationen an Mathematikerinnen und Mathematiker daran vergeblich ihre Zähne ausgebissen hatten, glaubte der pensionierte Druckanlagentechniker David Smith aus Yorkshire im November 2022, solch eine Einstein-Kachel gefunden zu haben.
Smith zeigte die Kachel dem mathematikbegeisterten Informatiker Graig Kaplan von der University of Waterloo, der schnell das Potenzial der Fliese erkannte. Zusammen mit dem Softwareentwickler Joseph Samuel Myers und dem Mathematiker Chaim Goodman-Strauss von der University of Arkansas gelang tatsächlich der Beweis, dass sich mit der Fliese tatsächlich eine Ebene lückenlos pflastern lässt, ohne dass sich das Muster einmal wiederholt.
Die Forschenden fanden jedoch noch viel mehr heraus: Smith hatte nicht nur eine Einstein-Kachel gefunden, sondern zugleich unendlich viele. Die Kanten der dreizehnseitigen Kachel lassen sich beliebig vergrößern oder verkleinern und stets ist es möglich, unendlich viele Muster damit zu verlegen. Die Ergebnisse ihrer Forschungen haben die vier Genannten in einer noch nicht begutachteten Arbeit veröffentlicht.
Die Suche nach einem Einstein
Die Suche nach dem Einstein hat sich im Laufe der Jahre entwickelt, ursprünglich ging es um eine andere Fragestellung: „Wie viele Kacheln braucht es mindestens, um eine aperiodische Parkettierung zu erzeugen?“ Bereits 1966 hat sich der Mathematiker Robert Berger damit beschäftigt und kam letztlich auf 104 unterschiedliche Kacheln, die ein aperiodisches Muster erzeugen. Der Informatiker Donald Knuth verbesserte diesen Wert im Jahr 1968 auf 92 Kacheln. Doch bereits ein Jahr später veröffentlichte der Mathematiker Rafael Robinson eine Variante mit lediglich sechs Fliesentypen.
Lange Jahre hielt der Physiker Roger Penrose den Bestwert, der 1974 eine Lösung mit nur zwei Kacheln präsentierte. Seit dieser Zeit fragt sich die Fachwelt, ob es nicht auch möglich ist, mit nur einer Kachelform eine Ebene so zu überdecken, ohne dass jemals ein periodisches Muster entsteht. Nach vielen Jahrzehnten der erfolglosen Tüftelei und Rechnerei zahlreicher Naturwissenschaftlerinnen und Naturwissenschaftlern, knackte der Frührentner David Smith den heiligen Gral und fand einen Einstein.
Nach Berichten der „New York Times“ nutzte Smith dafür die Software „PolyForm Puzzle Solver“. Mit diesem Programm lassen sich Kacheln entwerfen und zusammensetzen, so dass eine große Fläche entsteht – ähnlich einem Fliesenboden. Fand der Tüftler eine Form vielversprechend, druckte er sie aus, vervielfältigte sie. Nach dem Ausschneiden der Form konnte er dann nach Belieben puzzeln. So kam er schließlich auf die Form, die sich letztlich als Einstein entpuppte. Sie besteht aus 13 Ecken und Kanten und hat eine gewisse Ähnlichkeit mit einem Hut, weshalb Smith sie als „Hat“ bezeichnete.
Nachweis der Einstein-Kachel
David Smith konnte nur vermuten, dass es sich bei der entdeckten Kachel um einen Einstein handelt. In der Wissenschaft braucht es daher einen mathematischen Beweis. Hier kommen die bereits genannten Graig Kaplan, Joseph Samuel Myers und Mathematiker Chaim Goodman-Strauss ins Spiel. Die beiden letztgenannten hatten sich bereits in der Vergangenheit mit Kachelungen beschäftigt, weshalb Kaplan sie mit ins Boot genommen hat. Die beiden waren anfangs recht erstaunt über die einfache Form, wie Goodman-Strauss dem renommierten Wissenschaftsportal „ScienceNews“ erzählte.
Nicht nur die einfache Form überraschte die Forschenden, sie fanden zudem heraus, dass sie mit den Längen der Seiten spielen können und immer noch ein aperiodisches Muster vorfinden, das lückenlos ist. Sie hatten damit nicht nur eine mögliche Einstein-Kachel vor sich, sondern gleich unendlich viele. Um einen stichhaltigen Beweis zu führen, dass es sich bei der Form tatsächlich um einen Einstein handelt, stützten sich die Wissenschaftler auf bewährte Methoden, die bereits seit Jahrzehnten von Fachleuten genutzt werden, Myers entwickelte darüber hinaus eine vollkommen neue Beweismethode.
Methode 1:
Bei der ersten Methode, die auf bereits zuvor durchgeführte Berechnungen für andere Kacheln basiert, untersuchten die Forscher nicht direkt den Hut selbst, sondern vier verschiedene Cluster, die aus mehreren Kacheln bestehen. Diese Cluster bestehen aus einem Sechseck, einem Fünfeck, einem Parallelogramm und einem Dreieck, die jeweils passend zusammengefügt eine lückenlose Ebene ergeben.
Doch das ist noch nicht alles, denn wenn man die Cluster-Polygone wiederum kombiniert, entsteht eines der vier größeren Polygone. Dieses kann nur aus einer bestimmten Anordnung der kleineren Cluster-Polygone entstehen und ist somit einzigartig. Durch die Kombination dieser größeren Polygone kann man immer größere Strukturen bilden, die sich aus einer eindeutigen Anordnung der kleineren Polygone zusammensetzen. Auf diese Weise wird Periodizität ausgeschlossen, da sich immer größere Polygone erzeugen lassen, die ihre Einzigartigkeit behalten.
Dieser Beweis lässt sich nicht nur auf den von Smith vorgestellten Hut anwenden, sondern auch auf andere Variationen der Kachel. Es ist faszinierend zu sehen, wie sich aus einfachen geometrischen Formen eine hierarchische Struktur ergibt, die niemals periodisch wird.
Methode 2:
Myers wollte mehr wissen und fand heraus, dass die Hut-Kachelung mit zwei anderen Parkettierungen aus sogenannten Polydiamanten zusammenhängt. Diese geometrischen Formen bestehen aus gleichseitigen Dreiecken. Wenn diese beiden Pflasterungen aperiodisch sind, hat die Hut-Kachel automatisch dieselben Eigenschaften. Und das Beste daran: Myers konnte dies alles ohne einen Computer beweisen!
Er untersuchte die Polydiamanten-Systeme und fand heraus, dass sie nicht periodisch sind. Wenn etwas periodisch ist, gibt es Verschiebungsvektoren, die einen Bereich der Parkettierung auf einen identischen überführen. Die Verschiebungsvektoren der beiden Polydiamanten-Pflasterungen müssten sich laut Myers um einen rationalen Faktor (eine Bruchzahl) unterscheiden. Aber Myers fand ein Verhältnis von √2 – eine irrationale Zahl. Irrationale Werte in Parkettierungen deuten meist auf Aperiodizität hin. Das bedeutet, dass sich ein Muster nicht wiederholt. Myers hat also bewiesen, dass die Hut-Kachel aperiodisch ist.
Die vollständige Forschungsarbeit mit der kompletten Beweisführung finden Sie hier.
Die Einstein-Kachel im Fokus der Physik
Die Entdeckung der neuen Form löste im vergangenen Jahr Begeisterung unter Mathematikliebhabern aus, ohne dass sofort eine praktische Anwendung ersichtlich war. Mathematische Konzepte mit ästhetischem Wert finden jedoch oft unerwartete Anwendungen in der Physik, wie die Geschichte der oben beschriebenen „Penrose-Parkettierungen“ zeigt.
Diese fanden ihre Entsprechung in den Quasikristallen des Chemie-Nobelpreisträgers Daniel Shechtman. Quasikristalle, eine Art Zwischenform von Kristallen und amorphen Materialien, sind geordnet, aber nicht periodisch. Shechtmans Theorie stieß zunächst auf Widerstand, erwies sich aber schließlich als richtig.
Eine Forschungsgruppe unter der Leitung von Adolfo Grushin am französischen Nationalen Zentrum für wissenschaftliche Forschung (CNRS) untersuchte in den vergangenen Monaten die Eigenschaften eines Kristallgitters, das der Einstein-Kachel ähnelt. Die überraschenden Ergebnisse dieser Studie wurden von der Fachzeitschrift „Physical Review Letters“ zur Veröffentlichung angenommen.
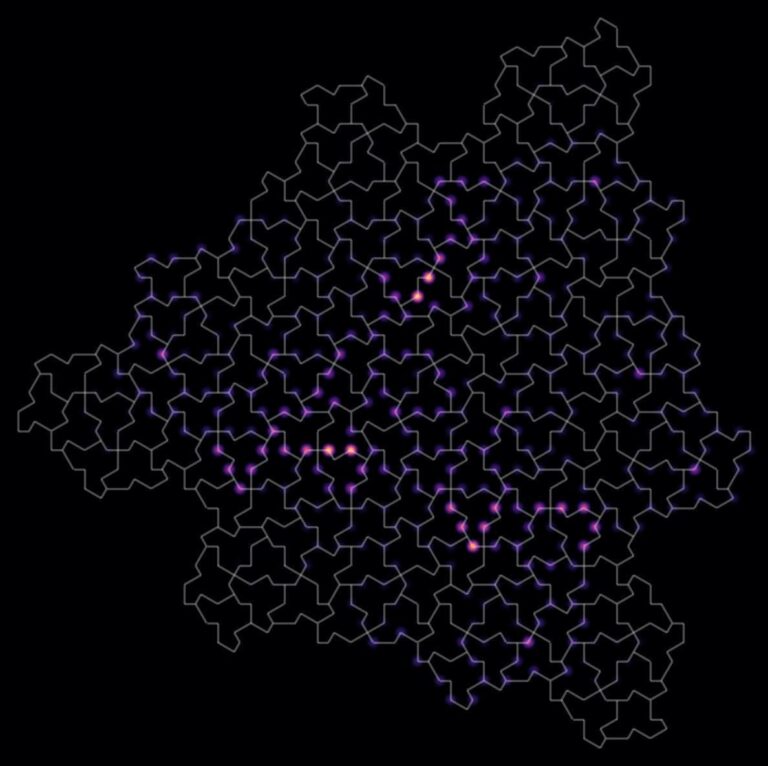
Visualisierung der Elektronenverteilung in einem Kristallgitter nach dem Vorbild der Einstein-Kachel.
Foto: A. Grushin/Institut NÉEL/CNRS
Ähnlichkeit mit Graphen
In ihrer Studie stellten die Forschenden fest, dass die Spektralfunktion des untersuchten Materials bemerkenswerte Parallelen zu Graphen aufweist, insbesondere eine hexagonale Symmetrie. Dies steht im Gegensatz zu den von Shechtman entdeckten Quasikristallen, die typischerweise eine fünfeckige Symmetrie aufweisen. Graphen besteht aus Kohlenstoffatomen, die wabenförmig angeordnet sind.
Im Gegensatz zu Graphen ändern sich die Eigenschaften des Materials jedoch, wenn es reflektiert wird, was auf seine Chiralität zurückzuführen ist. Diese Eigenschaft beeinflusst die optischen Eigenschaften des Materials. Obwohl das Material viele Eigenschaften mit Quasikristallen teilt, verhält es sich überraschend ähnlich wie herkömmliche Kristalle. Darauf weist die Physikerin Sinéad Griffin vom Lawrence Berkeley National Laboratory in Kalifornien in einem Kommentar gegenüber „Science News“ hin. Sie war allerdings nicht an der Studie beteiligt.
Überraschender Effekt
Das Forschungsteam fand außerdem heraus, dass ein unerwarteter Effekt auftritt, wenn ein bestimmtes Magnetfeld angelegt wird. Um eine Fläche vollständig mit Einstein-Kacheln zu bedecken, müssen einige dieser Kacheln gespiegelt werden. In der Nähe dieser gespiegelten Kacheln sammeln sich Elektronen und werden eingefangen. „
Dieses Phänomen fanden wir sehr ästhetisch“, erklärt Studienleiter Grushin. Obwohl dieses Material in der Natur noch nicht gefunden wurde, sieht Grushins Team die Möglichkeit, es künstlich herzustellen, indem man die Moleküle einzeln in einem Einstein-Muster auf einer Oberfläche anordnet. Einem Laien dürfte eine solche Entdeckung allerdings kaum gelingen. Smiths Entdeckung der Einstein-Kachel ist laut Forschungsteam eine Ausnahme gewesen.
Ein Beitrag von: