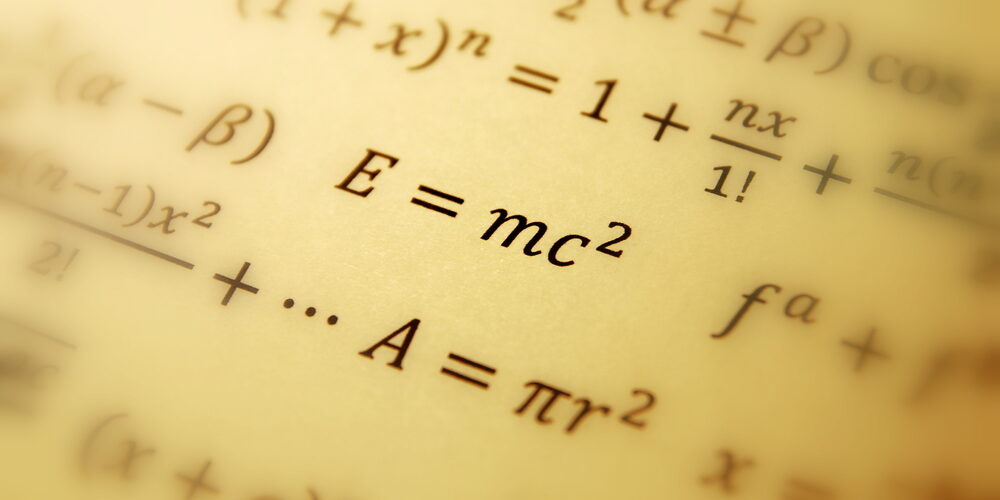Wie schwer ist Energie? Einstein gibt die Antwort
Wenn eine Feder gespannt wird, nimmt ihr Gewicht zu. Das ist mit den heute zur Verfügung stehenden technischen Mitteln allerdings nicht messbar. Wie verhält es sich mit einer Batterie? Wiegt eine aufgeladene Batterie mehr als eine entladene? Wenn ja, warum? Albert Einstein gibt die Antwort.
Albert Einsteins berühmteste Formel besagt, dass zwischen der Masse und Energie eine feste Verbindung besteht.
Foto: Panthermedia.net/AndreyPopov
Die Gleichung E=m*C² ist vermutlich die bekannteste mathematische Beziehung weltweit. Sie stammt von Albert Einstein, der sie 1905 veröffentlichte. Diese Gleichung zeigt die Äquivalenz von Energie (E) und Masse (m) auf, wobei sie durch das Quadrat der Lichtgeschwindigkeit (c²) verbunden sind. Das bedeutet, dass Energie tatsächlich eine „Masse“ oder ein „Gewicht“ haben kann, auch wenn es vielleicht schwer zu verstehen ist. Wahrscheinlich hat noch keiner nach dem Aufladen des Smartphones gedacht, dass dieses nur schwerer als zuvor sei.
Ist ein geladener Akku im E-Auto schwerer als ein leerer?
Bei einem traditionellen Auto mit Verbrennungsmotor ist es offensichtlich: Wenn man volltankt, erhöht sich das Gewicht des Fahrzeugs. Jeder Liter Benzin bringt fast drei Viertel eines Kilogramms auf die Waage, was bedeutet, dass das Auto nach dem Tanken um etwa 50 Kilo schwerer sein kann. Wenn dieser Kraftstoff verbrannt wird, wird seine Masse in die Umwelt freigesetzt und das Auto wird leichter.
Doch wie verhält es sich mit Elektroautos? Intuitiv würden wir denken, dass die Energie in der Batterie das Gewicht des Autos nicht beeinflusst. Beim Laden und Entladen werden schließlich nur chemische Reaktionen ausgelöst, ohne dass Material hinzugefügt oder entfernt wird. Dies wird durch unsere tägliche Erfahrung mit Smartphones bestätigt, die unabhängig von ihrem Ladezustand stets das gleiche Gewicht aufweisen.
Allerdings bringt Einsteins berühmte Gleichung E=m*C² eine interessante Wendung in diese Überlegung. Wenn man die Gleichung umstellt, erhält man m=E/C², was bedeutet, dass ein geladener Akku tatsächlich ein wenig mehr wiegt. Auch wenn dieser Unterschied minimal und nicht messbar ist, ist er theoretisch vorhanden. Das wirft die Frage auf: Wie kam Einstein zu dieser bahnbrechenden Gleichung und wie konnte er überzeugt sein, dass Energie eine Masse hat, selbst wenn sich nicht messen lässt?
Licht spielt eine wesentliche Rolle
Licht breitet sich stets mit einer konstanten Geschwindigkeit von etwa 300.000 Kilometern pro Sekunde aus, unabhängig von der Bewegung seiner Quelle. Dies ist bei Schall unterschiedlich: Schallwellen benötigen ein Medium zur Ausbreitung, in der Regel Luft, und ihre Geschwindigkeit variiert je Medium, aber auch je nach Temperatur oder je nach Geschwindigkeit der Schallquelle relativ zum Beobachter.
So hört sich das Geräusch eines fahrenden Zuges zum Beispiel anders an, wenn er sich Ihnen nähert oder wenn er sich von Ihnen entfernt. Das nennt sich dann Dopplereffekt. Wenn er näher kommt, erhöht sich die Frequenz und damit die Tonhöhe. Wenn er sich entfernt, sinkt die Frequenz und auch die Tonhöhe.
Im Gegensatz dazu benötigt Licht keinen physischen Träger für seine Ausbreitung; es kann sich sogar im Vakuum bewegen. Tatsächlich stellt die Lichtgeschwindigkeit das absolute Tempolimit im Universum dar – nichts kann sich schneller bewegen. Aus diesem Verhalten des Lichts ergibt sich auch die berühmte Gleichung von Einstein: E=m*C².
Ein Gedankenexperiment half Einstein
Albert Einstein gelangte zu seiner vielleicht bekanntesten Gleichung durch ein einfaches Gedankenexperiment und mathematische Überlegungen: Stellen Sie sich ein ruhendes Objekt vor, das plötzlich zwei gleiche Lichtblitze in entgegengesetzte Richtungen aussendet. Obwohl das Objekt an Ort und Stelle bleibt, verliert es Energie aufgrund der abgegebenen Lichtblitze.
Einstein überlegte weiter: Wie würde dieser Vorgang für einen Beobachter aussehen, der sich bewegt? Aus der Sicht dieses Beobachters würde das Objekt geradlinig an ihm vorüberziehen, während die Lichtblitze in verschiedene Richtungen flitzen. Obwohl beide Blitze mit Lichtgeschwindigkeit reisen, erscheinen sie energetisch unterschiedlich. Der Blitz, der in Bewegungsrichtung des Beobachters reist, scheint mehr Energie zu besitzen als der entgegengerichtete Blitz.
Nach weiteren mathematischen Überlegungen kam Einstein zu dem Schluss, dass, wenn ein Objekt Energie in Form von Licht verliert, es auch an Masse verlieren muss. Dies implizierte, dass Masse und Energie ineinander umgewandelt werden können – daher E=m*C².
Die Bedeutung dieser Erkenntnis war immens, sowohl auf mikroskopischer Ebene als auch im größeren Kontext des Universums. Leider führte diese Erkenntnis auch zu Entwicklungen wie der Kernspaltung und der Erschaffung einer der zerstörerischsten Waffen: der Atombombe.
Sechzig 1-Euro-Münzen reichen aus, um alle Kraftwerke abschalten zu können
Nimmt man die Formel von Einstein zur Hand, lässt sich leicht errechnen, dass selbst in kleinen Massen gewaltige Energien stecken: So wiegt ein Euro-Stück zwar gerade einmal sieben Gramm beziehungsweise 7 × 10-3 kg. Nach Einsteins Energie-Masse-Beziehung E=m*C² steckt in dieser Münze eine Energie von 6,3 × 1014 J.
Zur Veranschaulichung: Der durchschnittliche Tagesenergieverbrauch Deutschlands beträgt etwa 40 Petajoule oder 40 × 10^15 Joule. Basierend darauf würden nur sechzig Euro-Stücke, vollständig in Energie umgewandelt, genügen, um den Energiebedarf des Landes für einen ganzen Tag zu decken. Das entspricht etwa 75 Millionstel Eurocent pro Bürger täglich. Es wäre somit theoretisch ziemlich „einfach“, sich von sämtlichen Kohle-, Gas- oder Erdölabhängigkeiten zu verabschieden. Aber leider (oder auch Gott sei Dank) nur in der Theorie.
Wie lässt sich diese Energie freisetzen?
Die in einer Münze enthaltene Energie, wenn sie vollständig freigesetzt würde, hätte eine verheerende und potenziell katastrophale Auswirkung. Doch die Natur hat vorgesorgt: Im Gegensatz zur leicht freisetzbaren chemischen Energie in Sprengstoffen, ist die Umwandlung von Massenenergie, wie sie in E=m*C² beschrieben wird, nur durch atomare Vorgänge möglich.
Im größeren Maßstab erfolgt diese Umwandlung nur teilweise, wie etwa bei Kollisionen von Atomen mit hoher kinetischer Energie, beim Zerfall von Elektronen, Mesonen und anderen subatomaren Teilchen, bei der Fusion von Protonen und Neutronen zu schwereren Atomkernen oder bei der Spaltung von schweren Kernen, wie Uran oder Plutonium. In anderen Worten: Um diese Energie zu nutzen, bedarf es beträchtlicher wissenschaftlicher und technischer Anstrengungen.
Ein Beitrag von: